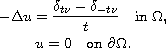Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 230, pp. 1-12.
Anisotropic singularity of solutions to elliptic
equations in a measure framework
Wanwan Wang, Huyuan Chen, Jian Wang
Abstract:
In this article we study the weak solutions of elliptic equation
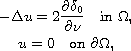
where
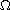 is an open bounded
is an open bounded
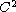 domain of
domain of
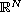 with
with
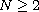 containing the origin,
containing the origin,
 is a unit vector and
is a unit vector and
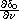 is defined in the distribution sense,
i.e.
is defined in the distribution sense,
i.e.
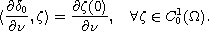
We prove that this problem admits a unique weak solution u in the sense that
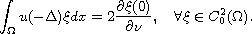
Moreover, u has an anisotropic singularity and can be approximated, as
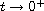 ,
by the solutions of
,
by the solutions of
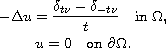
Submitted May 11, 2015. Published September 10, 2015.
Math Subject Classifications: 35R06, 35B40, 35Q60.
Key Words: Anisotropy singularity; weak solution; uniqueness.
Show me the PDF file (250 KB),
TEX file, and other files for this article.
 |
Wanwan Wang
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: wwwang2014@yeah.net
|
|---|
 |
Huyuan Chen
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: chenhuyuan@yeah.net
|
|---|
 |
Jian Wang
Institute of Technology
East China Jiaotong University
Nanchang, Jiangxi 330022, China
email: jianwang2007@126.com
|
|---|
Return to the EJDE web page
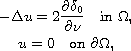
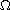 is an open bounded
is an open bounded
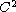 domain of
domain of
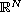 with
with
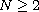 containing the origin,
containing the origin,
 is a unit vector and
is a unit vector and
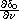 is defined in the distribution sense,
i.e.
is defined in the distribution sense,
i.e.
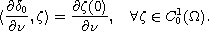
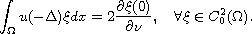
 ,
by the solutions of
,
by the solutions of