Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 227, pp. 1-10.
Nonexistence of global solutions of some nonlinear
space-nonlocal evolution equations on the Heisenberg group
Bashir Ahmad, Ahmed Alsaedi, Mokhtar Kirane
Abstract:
This article presents necessary conditions for the existence of weak solutions
of the following space-nonlocal evolution equations on
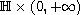 , where
, where
 is the Heisenberg group:
is the Heisenberg group:
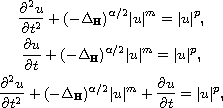
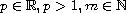 .
Moreover, the life span
for each equation is estimated under some suitable conditions.
Our method of proof is based on the test function method.
.
Moreover, the life span
for each equation is estimated under some suitable conditions.
Our method of proof is based on the test function method.
Submitted August 19, 2015. Published September 2, 2015.
Math Subject Classifications: 35A01, 35R03, 35R11
Key Words: Nonlinear hyperbolic equations; nonlinear parabolic equations;
nonlocal operators; damping; blowing-up solutions.
Show me the PDF file (245 KB),
TEX file, and other files for this article.
 |
Bashir Ahmad
Nonlinear Analysis and Applied Mathematics (NAAM) Research Group
Department of Mathematics, Faculty of Science
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: bashirahmad_qau@yahoo.com
|
|---|
| |
Ahmed Alsaedi
Nonlinear Analysis and Applied Mathematics (NAAM) Research Group
Department of Mathematics, Faculty of Science
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: aalsaedi@hotmail.com
|
|---|
 |
Mokhtar Kirane
Laboratoire de Mathématiques, Image et Applications
Université de La Rochelle,
Avenue M. Crépeau
17042 La Rochelle Cedex, France
email: mokhtar.kirane@univ-lr.fr
|
|---|
Return to the EJDE web page
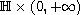 , where
, where
 is the Heisenberg group:
is the Heisenberg group:
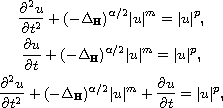
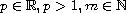 .
Moreover, the life span
for each equation is estimated under some suitable conditions.
Our method of proof is based on the test function method.
.
Moreover, the life span
for each equation is estimated under some suitable conditions.
Our method of proof is based on the test function method.

