In this article, we study a time-independent fractional Schrodinger equation with non-local (regional) diffusion
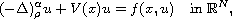
where
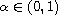 ,
,
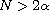 .
We establish the existence of a
non-negative ground state solution by variational methods.
.
We establish the existence of a
non-negative ground state solution by variational methods.
Yang Pu, Jiu Liu, Chun-Lei Tang
Abstract:
In this article, we study a time-independent fractional
Schrodinger equation with non-local (regional) diffusion
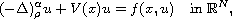
where
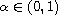 ,
,
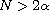 .
We establish the existence of a
non-negative ground state solution by variational methods.
.
We establish the existence of a
non-negative ground state solution by variational methods.
Submitted June 15, 2015. Published August 28, 2015.
Math Subject Classifications: 35J60, 35J20
Key Words: Nonlinear Schrodinger equation; fractional Laplacian;
non-local operator; ground state solution.
Show me the PDF file (257 KB), TEX file, and other files for this article.
 |
Yang Pu School of Mathematics and Statistics Southwest University Chongqing 400715, China email: pt8820@swu.edu.cn |
|---|---|
 |
Jiu Liu School of Mathematics and Statistics Southwest University Chongqing 400715, China email: jiuliu2011@163.com |
 |
Chun-Lei Tang School of Mathematics and Statistics Southwest University Chongqing 400715, China Phone +86 23 68253135, fax +86 23 68253135 email: tangcl@swu.edu.cn |
Return to the EJDE web page