Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 22, pp. 1-8.
Entire solutions for nonlinear differential-difference equations
Na Xu, Ting-Bin Cao, Kai Liu
Abstract:
In this article, we study entire solutions of the nonlinear
differential-difference equation
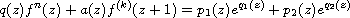
where
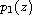 ,
,
 are nonzero polynomials,
are nonzero polynomials,
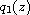 ,
,
 are nonconstant polynomials,
are nonconstant polynomials,
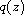 ,
,
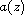 are nonzero entire functions of finite order,
are nonzero entire functions of finite order,
 is an integer. We obtain additional results for
case:
is an integer. We obtain additional results for
case:
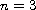 ,
,
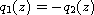 ,
and
,
and
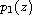 ,
,
 nonzero constants.
nonzero constants.
Submitted July 15, 2014. Published January 27, 2015.
Math Subject Classifications: 30D35, 39A05.
Key Words: Nevanlinna theory; differential-difference equation; entire function.
Show me the PDF file (206 KB),
TEX file, and other files for this article.
 |
Na Xu
School of Mathematical Sciences, Xiamen University
Xiamen 361005, China
email: xuna406@163.com
|
|---|
 |
Ting-Bin Cao
Department of Mathematics, Nanchang University
Nanchang, Jiangxi 330031, China
email: tbcao@ncu.edu.cn
|
|---|
 |
Kai Liu
Department of Mathematics, Nanchang University
Nanchang, Jiangxi 330031, China
email: liukai418@126.com
|
|---|
Return to the EJDE web page
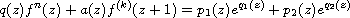
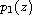 ,
,
 are nonzero polynomials,
are nonzero polynomials,
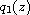 ,
,
 are nonconstant polynomials,
are nonconstant polynomials,
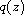 ,
,
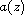 are nonzero entire functions of finite order,
are nonzero entire functions of finite order,
 is an integer. We obtain additional results for
case:
is an integer. We obtain additional results for
case:
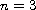 ,
,
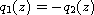 ,
and
,
and
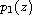 ,
,
 nonzero constants.
nonzero constants.


