Based on Ekeland's variational principle and the mountain pass theorem, we show the existence of three solutions to the Kirchhoff type problem
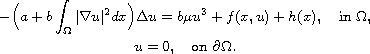
Where the parameter
 is sufficiently close,
from the left, to the first nonlinear eigenvalue.
is sufficiently close,
from the left, to the first nonlinear eigenvalue.
Shu-Zhi Song, Chun-Lei Tang, Shang-Jie Chen
Abstract:
Based on Ekeland's variational principle and the mountain pass theorem,
we show the existence of three solutions to the Kirchhoff type problem
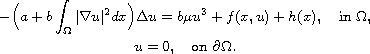
Where the parameter
 is sufficiently close,
from the left, to the first nonlinear eigenvalue.
is sufficiently close,
from the left, to the first nonlinear eigenvalue.
Submitted March 23, 2015. Published August 17, 2015.
Math Subject Classifications: 35J61, 35C06, 35J20.
Key Words: Near resonance; mountain pass theorem; Kirchhoff type;
Ekeland's variational principle.
Show me the PDF file (209 KB), TEX file, and other files for this article.
 |
Shu-Zhi Song School of Mathematics and Statistics Southwest University Chongqing 400715, China email: sjrdj@163.com |
|---|---|
 |
Chun-Lei Tang School of Mathematics and Statistics Southwest University Chongqing 400715, China email: tangcl@swu.edu.cn, Tel +8613883159865 |
 |
Shang-Jie Chen School of Mathematics and Statistics Chongqing Technology and Business University Chongqing 400067, China email: chensj@ctbu.edu.cn, 11183356@qq.com |
Return to the EJDE web page