Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 213, pp. 1-15.
Asymptotically linear Schrodinger equation with zero on the
boundary of the spectrum
Dongdong Qin, Xianhua Tang
Abstract:
This article concerns the Schrodinger equation
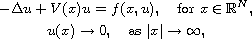
where V and f are periodic in x, and 0 is a boundary point of
the spectrum
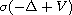 .
Assuming that f(x,u) is asymptotically
linear as
.
Assuming that f(x,u) is asymptotically
linear as
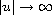 ,
existence of a ground state solution is established
using some new techniques.
,
existence of a ground state solution is established
using some new techniques.
Submitted January 18, 2015. Published August 17, 2015.
Math Subject Classifications: 35J20, 35J60, 35Q55.
Key Words: Schrodinger equation; strongly indefinite functional;
spectrum point zero; asymptotically linear; ground states solution.
Show me the PDF file (295 KB),
TEX file, and other files for this article.
 |
Dongdong Qin
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: qindd132@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
Return to the EJDE web page
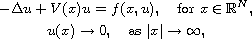
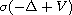 .
Assuming that f(x,u) is asymptotically
linear as
.
Assuming that f(x,u) is asymptotically
linear as
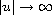 ,
existence of a ground state solution is established
using some new techniques.
,
existence of a ground state solution is established
using some new techniques.

