Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 211, pp. 1-10.
Critical exponent for a damped wave system with fractional integral
Mijing Wu, Shengjia Li, Liqing Lu
Abstract:
We shall present the critical exponent
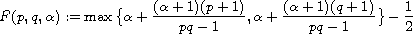
for the Cauchy problem
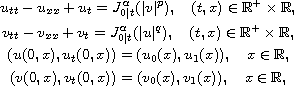
where
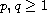 ,
,
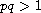 and
and
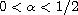 ;
that is, the small data global
existence of solutions can be derived to the problem above if
;
that is, the small data global
existence of solutions can be derived to the problem above if
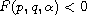 .
Furthermore, in the case of
.
Furthermore, in the case of
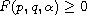 the non-existence of global
solution can be obtained with the initial data having positive average value.
the non-existence of global
solution can be obtained with the initial data having positive average value.
Submitted July 24, 2015. Published August 12, 2015.
Math Subject Classifications: 35B33.
Key Words: Damped wave equation; fractional integral;
critical exponent; global solution.
Show me the PDF file (254 KB),
TEX file, and other files for this article.
 |
Mijing Wu
School of Mathematical Sciences
Shanxi University
Taiyuan, Shanxi 030006, China
email: mjwu@sxu.edu.cn
|
|---|
 |
Shengjia Li
School of Mathematical Sciences
Shanxi University
Taiyuan, Shanxi 030006, China
email: sjli@sxu.edu.cn
|
|---|
 |
Liqing Lu
School of Mathematical Sciences
Shanxi University
Taiyuan, Shanxi 030006, China
email: lulq@sxu.edu.cn
|
|---|
Return to the EJDE web page
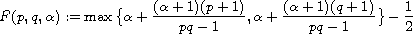
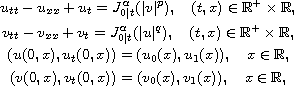
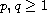 ,
,
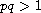 and
and
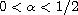 ;
that is, the small data global
existence of solutions can be derived to the problem above if
;
that is, the small data global
existence of solutions can be derived to the problem above if
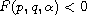 .
Furthermore, in the case of
.
Furthermore, in the case of
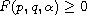 the non-existence of global
solution can be obtained with the initial data having positive average value.
the non-existence of global
solution can be obtained with the initial data having positive average value.


