Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 194, pp. 1-10.
Spectral analysis for the exceptional Xm-Jacobi equation
Constanze Liaw, Lance Littlejohn, Jessica Stewart Kelly
Abstract:
We provide the mathematical foundation for the
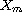 -Jacobi
spectral theory.
Namely, we present a self-adjoint operator associated to the differential
expression with the exceptional
-Jacobi
spectral theory.
Namely, we present a self-adjoint operator associated to the differential
expression with the exceptional
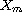 -Jacobi
orthogonal polynomials as
eigenfunctions. This proves that those polynomials are indeed eigenfunctions
of the self-adjoint operator (rather than just formal eigenfunctions).
Further, we prove the completeness of the exceptional
-Jacobi
orthogonal polynomials as
eigenfunctions. This proves that those polynomials are indeed eigenfunctions
of the self-adjoint operator (rather than just formal eigenfunctions).
Further, we prove the completeness of the exceptional
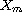 -Jacobi orthogonal
polynomials (of degrees
-Jacobi orthogonal
polynomials (of degrees
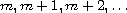 )
in the Lebesgue-Hilbert space
with the appropriate weight. In particular, the self-adjoint operator has no
other spectrum.
)
in the Lebesgue-Hilbert space
with the appropriate weight. In particular, the self-adjoint operator has no
other spectrum.
Submitted February 6, 2015. Published July 27, 2015.
Math Subject Classifications: 33C45, 34B24, 33C47, 34L05.
Key Words: Exceptional orthogonal polynomial; spectral theory;
self-adjoint operator; Darboux transformation.
Show me the PDF file (219 KB),
TEX file, and other files for this article.
 |
Constanze Liaw
Department of Mathematics and CASPER
Baylor University, One Bear Place #97328
Waco, TX 76798-7328, USA
email: Constanze_Liaw@baylor.edu
|
|---|
 |
Lance Littlejohn
Department of Mathematics, Baylor University
One Bear Place #97328
Waco, TX 76798-7328, USA
email: Lance_Littlejohn@baylor.edu
|
|---|
 |
Jessica Stewart Kelly
Department of Mathematics
Christopher Newport University
1 Avenue of the Arts
Newport News, VA 23606, USA
email: Jessica.Stewart@cnu.edu
|
|---|
Return to the EJDE web page
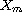 -Jacobi
spectral theory.
Namely, we present a self-adjoint operator associated to the differential
expression with the exceptional
-Jacobi
spectral theory.
Namely, we present a self-adjoint operator associated to the differential
expression with the exceptional
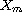 -Jacobi
orthogonal polynomials as
eigenfunctions. This proves that those polynomials are indeed eigenfunctions
of the self-adjoint operator (rather than just formal eigenfunctions).
Further, we prove the completeness of the exceptional
-Jacobi
orthogonal polynomials as
eigenfunctions. This proves that those polynomials are indeed eigenfunctions
of the self-adjoint operator (rather than just formal eigenfunctions).
Further, we prove the completeness of the exceptional
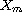 -Jacobi orthogonal
polynomials (of degrees
-Jacobi orthogonal
polynomials (of degrees
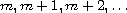 )
in the Lebesgue-Hilbert space
with the appropriate weight. In particular, the self-adjoint operator has no
other spectrum.
)
in the Lebesgue-Hilbert space
with the appropriate weight. In particular, the self-adjoint operator has no
other spectrum.


