Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 187, pp. 1-26.
Singular limit solutions for 4-dimensional stationary
Kuramoto-Sivashinsky equations with exponential nonlinearity
Sami Baraket, Moufida Khtaifi, Taieb Ouni
Abstract:
Let
 be a bounded domain in
be a bounded domain in
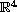 with smooth boundary, and
let
with smooth boundary, and
let
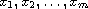 be points in
be points in
 .
We are concerned with the singular stationary non-homogenous
Kuramoto-Sivashinsky equation
.
We are concerned with the singular stationary non-homogenous
Kuramoto-Sivashinsky equation
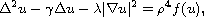
where f is a function that depends only the spatial variable. We
use a nonlinear domain decomposition method to give sufficient
conditions for the existence of a positive weak solution satisfying
the Dirichlet-like boundary conditions
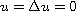 ,
and being
singular at each
,
and being
singular at each
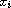 as the parameters
as the parameters
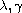 and
and
 tend to 0. An analogous problem in two-dimensions was
considered in [2] under condition (A1) below. However we do
not assume that condition.
tend to 0. An analogous problem in two-dimensions was
considered in [2] under condition (A1) below. However we do
not assume that condition.
Submitted January 28, 2015. Published July 13, 2015.
Math Subject Classifications: 58J08, 35J40, 35J60, 35J75.
Key Words: Singular limits; Green's function; Kuramoto-Sivashinsky equation;
domain decomposition method.
Show me the PDF file (373 KB),
TEX file, and other files for this article.
 |
Sami Baraket
Department of Mathematics, College of Science
King Saud University, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: sbaraket@ksu.edu.sa
|
|---|
 |
Moufida Khtaifi
Département de Mathématiques
Faculté des Sciences de Tunis Campus Universitaire
Université Tunis Elmanar, 2092 Tunis, Tunisia
email: moufida180888@gmail.com
|
|---|
 |
Taieb Ouni
Département de Mathématiques
Faculté des Sciences de Tunis Campus Universitaire
Université Tunis Elmanar, 2092 Tunis, Tunisia
email: Taieb.Ouni@fst.rnu.tn
|
|---|
Return to the EJDE web page
 be a bounded domain in
be a bounded domain in
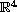 with smooth boundary, and
let
with smooth boundary, and
let
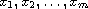 be points in
be points in
 .
We are concerned with the singular stationary non-homogenous
Kuramoto-Sivashinsky equation
.
We are concerned with the singular stationary non-homogenous
Kuramoto-Sivashinsky equation
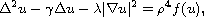
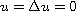 ,
and being
singular at each
,
and being
singular at each
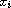 as the parameters
as the parameters
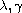 and
and
 tend to 0. An analogous problem in two-dimensions was
considered in [2] under condition (A1) below. However we do
not assume that condition.
tend to 0. An analogous problem in two-dimensions was
considered in [2] under condition (A1) below. However we do
not assume that condition.


