Electron. J. Diff. Equ., Vol. 2015 (2015), No. 182, pp. 1-7.

A Liouville type theorem for p-Laplace equations

Cristian Enache

Abstract:
In this note we study solutions defined on the whole space 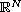$\mathbb{R}^N$ for the p-Laplace equation
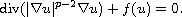
$$ \hbox{div}(| \nabla u|^{p-2}\nabla u)+f(u)=0. $$
Under an appropriate condition on the growth of f, which is weaker than conditions previously considered in McCoy [3] and Cuccu-Mhammed-Porru [1], we prove the non-existence of non-trivial positive solutions.

Submitted October 18, 2014. Published July 1, 2015.
Math Subject Classifications: 70H25.
Key Words: p-Laplace equation; Liouville theorem; entire solutions.

Show me the PDF file (184 KB), TEX file, and other files for this article.

Cristian Enache
Simion Stoilow Institute of Mathematics
of the Romanian Academy 010702
Bucharest, Romania
email: cenache23@yahoo.com

Return to the EJDE web page