Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 177, pp. 1-8.
Positive bounded solutions for semilinear elliptic systems
with indefinite weights in the half-space
Ramzi Alsaedi, Habib Maagli, Vicentiu Radulescu, Noureddine Zeddini
Abstract:
In this article, we study the existence and nonexistence of positive bounded
solutions of the Dirichlet problem
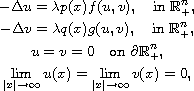
where
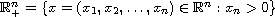 (
(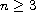 )
is the upper half-space and
)
is the upper half-space and
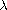 is a positive parameter.
The potential functions p,q are not necessarily bounded, they may change
sign and the functions
is a positive parameter.
The potential functions p,q are not necessarily bounded, they may change
sign and the functions
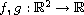 are continuous.
By applying the Leray-Schauder fixed point theorem, we establish the
existence of positive solutions for
are continuous.
By applying the Leray-Schauder fixed point theorem, we establish the
existence of positive solutions for
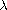 sufficiently small when
sufficiently small when
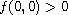 and
and
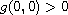 .
Some nonexistence results of positive bounded
solutions are also given either if
.
Some nonexistence results of positive bounded
solutions are also given either if
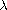 is sufficiently small
or if
is sufficiently small
or if
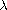 is large enough.
is large enough.
Submitted April 13, 2015. Published June 26, 2015.
Math Subject Classifications: 35B09, 35J47, 35J57, 58C30.
Key Words: Semilinear elliptic system; Leray-Schauder fixed point theorem;
positive bounded solution; indefinite potential.
Show me the PDF file (214 KB),
TEX file, and other files for this article.
 |
Ramzi Alsaedi
Department of Mathematics, Faculty of Sciences
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: ramzialsaedi@yahoo.co.uk
|
|---|
 |
Habib Mâaagli
Department of Mathematics, Faculty of Sciences
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: abobaker@kau.edu.sa
|
|---|
 |
Vicentiu Radulescu
Department of Mathematics, Faculty of Sciences
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: vicentiu.radulescu@imar.ro
|
|---|
 |
Noureddine Zeddini
Department of Mathematics, Faculty of Sciences
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: nalzeddini@kau.edu.sa
|
|---|
Return to the EJDE web page
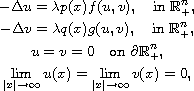
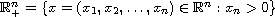 (
(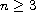 )
is the upper half-space and
)
is the upper half-space and
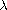 is a positive parameter.
The potential functions p,q are not necessarily bounded, they may change
sign and the functions
is a positive parameter.
The potential functions p,q are not necessarily bounded, they may change
sign and the functions
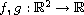 are continuous.
By applying the Leray-Schauder fixed point theorem, we establish the
existence of positive solutions for
are continuous.
By applying the Leray-Schauder fixed point theorem, we establish the
existence of positive solutions for
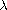 sufficiently small when
sufficiently small when
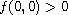 and
and
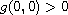 .
Some nonexistence results of positive bounded
solutions are also given either if
.
Some nonexistence results of positive bounded
solutions are also given either if
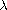 is sufficiently small
or if
is sufficiently small
or if
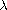 is large enough.
is large enough.



