Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 163, pp. 1-7.
Some relations between the Caputo fractional difference operators and
integer-order differences
Baoguo Jia, Lynn Erbe, Allan Peterson
Abstract:
In this article, we are concerned with the relationships between
the sign of Caputo fractional differences and integer nabla differences.
In particular, we show that if
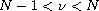 ,
,
 ,
,
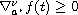 , for
, for
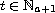 and
and
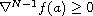 ,
then
,
then
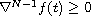 for
for
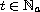 .
Conversely, if
.
Conversely, if
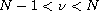 ,
,
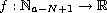 ,
and
,
and
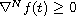 for
for
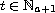 ,
then
,
then
 ,
for each
,
for each
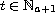 .
As applications of these two results, we get that
if
.
As applications of these two results, we get that
if
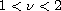 ,
,
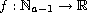 ,
,
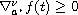 for
for
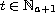 and
and
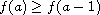 ,
then
,
then
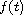 is an increasing function for
is an increasing function for
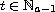 .
Conversely if
.
Conversely if
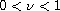 ,
,
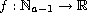 and
and
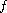 is an
increasing function for
is an
increasing function for
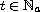 ,
then
,
then
 ,
for each
,
for each
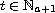 .
We also give a counterexample to show that the above assumption
.
We also give a counterexample to show that the above assumption
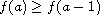 in the last result is essential.
These results demonstrate that, in some sense, the positivity of the
in the last result is essential.
These results demonstrate that, in some sense, the positivity of the
 -th order
Caputo fractional difference has a strong connection to the
monotonicity of
-th order
Caputo fractional difference has a strong connection to the
monotonicity of
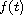 .
.
Submitted May 30, 2015. Published June 17, 2015.
Math Subject Classifications: 39A12, 39A70.
Key Words: Caputo fractional difference; monotonicity; Taylor monomial.
Show me the PDF file (185 KB),
TEX file, and other files for this article.
 |
Baoguo Jia
School of Mathematics and Computer Science
Sun Yat-Sen University
Guangzhou 510275, China
email: mcsjbg@mail.sysu.edu.cn
|
|---|
 |
Lynn Erbe
Department of Mathematics
University of Nebraska-Lincoln
Lincoln, NE 68588-0130, USA
email: lerbe2@math.unl.edu
|
|---|
 |
Allan Peterson
Department of Mathematics
University of Nebraska-Lincoln
Lincoln, NE 68588-0130, USA
email: apeterson1@math.unl.edu
|
|---|
Return to the EJDE web page
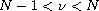 ,
,
 ,
,
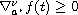 , for
, for
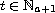 and
and
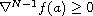 ,
then
,
then
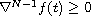 for
for
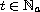 .
Conversely, if
.
Conversely, if
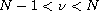 ,
,
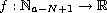 ,
and
,
and
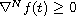 for
for
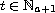 ,
then
,
then
 ,
for each
,
for each
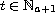 .
As applications of these two results, we get that
if
.
As applications of these two results, we get that
if
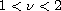 ,
,
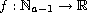 ,
,
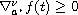 for
for
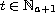 and
and
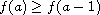 ,
then
,
then
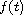 is an increasing function for
is an increasing function for
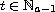 .
Conversely if
.
Conversely if
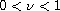 ,
,
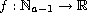 and
and
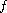 is an
increasing function for
is an
increasing function for
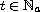 ,
then
,
then
 ,
for each
,
for each
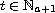 .
We also give a counterexample to show that the above assumption
.
We also give a counterexample to show that the above assumption
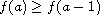 in the last result is essential.
These results demonstrate that, in some sense, the positivity of the
in the last result is essential.
These results demonstrate that, in some sense, the positivity of the
 -th order
Caputo fractional difference has a strong connection to the
monotonicity of
-th order
Caputo fractional difference has a strong connection to the
monotonicity of
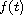 .
.


