Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 158, pp. 1-8.
Existence and non-existence of solutions for a p(x)-biharmonic problem
Ghasem A. Afrouzi, Maryam Mirzapour, Nguyen Thanh Chung
Abstract:
In this article, we study the following problem with Navier boundary
conditions
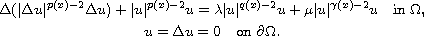
where
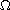 is a bounded domain in
is a bounded domain in
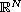 with smooth boundary
with smooth boundary
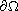 ,
,
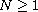 .
.
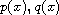 and
and
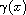 are continuous
functions on
are continuous
functions on
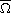 ,
,
 and
and
 are parameters.
Using variational methods, we establish some existence and non-existence
results of solutions for this problem.
are parameters.
Using variational methods, we establish some existence and non-existence
results of solutions for this problem.
Submitted July 22, 2014. Published June 15, 2015.
Math Subject Classifications: 35J60, 35B30, 35B40.
Key Words: p(x)-Biharmonic; variable exponent; critical points;
minimum principle; fountain theorem; dual fountain theorem.
Show me the PDF file (228 KB),
TEX file, and other files for this article.
 |
Ghasem A. Afrouzi
Department of Mathematics
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: afrouzi@umz.ac.ir
|
|---|
 |
Maryam Mirzapour
Department of Mathematics
Faculty of Mathematical Sciences
University of Mazandaran, Babolsar, Iran
email: mirzapour@stu.umz.ac.ir
|
|---|
 |
Nguyen Thanh Chung
Department of Mathematics,
Quang Binh University
312 Ly Thuong Kiet, Dong Hoi
Quang Binh, Vietnam
email: ntchung82@yahoo.com
|
|---|
Return to the EJDE web page
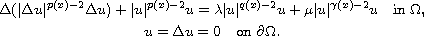
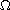 is a bounded domain in
is a bounded domain in
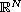 with smooth boundary
with smooth boundary
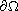 ,
,
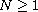 .
.
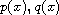 and
and
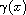 are continuous
functions on
are continuous
functions on
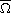 ,
,
 and
and
 are parameters.
Using variational methods, we establish some existence and non-existence
results of solutions for this problem.
are parameters.
Using variational methods, we establish some existence and non-existence
results of solutions for this problem.


