In this article we show the existence of at least one solution to the system of nonlocal resonant boundary-value problem
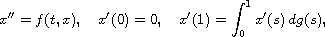
where
![$f:[0,1]\times\mathbb{R}^k\to\mathbb{R}^k$](gifs/ab.gif) ,
,
![$g:[0,1]\to\mathbb{R}^k$](gifs/ac.gif) .
.
Katarzyna Szymanska-Debowska
Abstract:
In this article we show the existence of at least one solution to
the system of nonlocal resonant boundary-value problem
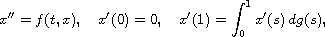
where
![$f:[0,1]\times\mathbb{R}^k\to\mathbb{R}^k$](gifs/ab.gif) ,
,
![$g:[0,1]\to\mathbb{R}^k$](gifs/ac.gif) .
.
Submitted February 2, 2015. Published June 6, 2015.
Math Subject Classifications: 34B10, 34B15.
Key Words: Nonlocal boundary value problem; perturbation method;
boundary value problem at resonance; Neumann BVP.
Show me the PDF file (211 KB), TEX file, and other files for this article.
 |
Katarzyna Szymanska-Debowska Institute of Mathematics Lodz University of Technology 90-924 Lodz, ul. Wolczanska 215, Poland email: katarzyna.szymanska-debowska@p.lodz.pl |
|---|
Return to the EJDE web page