Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 146, pp. 1-13.
Asymptotic behavior for small mass in an attraction-repulsion
chemotaxis system
Yuhuan Li, Ke Lin, Chunlai Mu
Abstract:
This article is concerned with the model
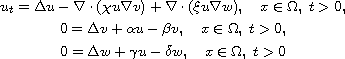
with homogeneous Neumann boundary conditions in a bounded domain
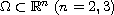 .
Under the critical condition
.
Under the critical condition
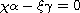 ,
we show that the system possesses a unique
global solution that is uniformly bounded in time. Moreover, when
,
we show that the system possesses a unique
global solution that is uniformly bounded in time. Moreover, when
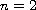 ,
by some appropriate smallness conditions on the initial data, we
assert that this solution converges to
(
,
by some appropriate smallness conditions on the initial data, we
assert that this solution converges to
(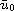 ,
,
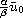 ,
,
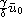 ) exponentially,
where
) exponentially,
where
 .
.
Submitted April 17, 2015. Published June 6, 2015.
Math Subject Classifications: 35A01, 35B40, 35K55, 92C17.
Key Words: Chemotaxis; attraction-repulsion; boundedness; convergence.
Show me the PDF file (269 KB),
TEX file, and other files for this article.
 |
Yuhuan Li
Department of Mathematics
Sichuan Normal University
Chengdu 610066, China
email: liyuhuanhuan@163.com
|
|---|
 |
Ke Lin
College of Mathematics and Statistics
Chongqing University
Chongqing 401331, China
email: shuxuelk@126.com
|
|---|
 |
Chunlai Mu
College of Mathematics and Statistics
Chongqing University
Chongqing 401331, China
email: clmu2005@163.com
|
|---|
Return to the EJDE web page
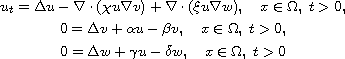
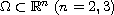 .
Under the critical condition
.
Under the critical condition
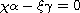 ,
we show that the system possesses a unique
global solution that is uniformly bounded in time. Moreover, when
,
we show that the system possesses a unique
global solution that is uniformly bounded in time. Moreover, when
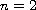 ,
by some appropriate smallness conditions on the initial data, we
assert that this solution converges to
(
,
by some appropriate smallness conditions on the initial data, we
assert that this solution converges to
(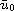 ,
,
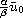 ,
,
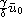 ) exponentially,
where
) exponentially,
where
 .
.


