Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 144, pp. 1-27.
Existence, uniqueness and stability of
traveling wavefronts for nonlocal dispersal equations with
convolution type bistable nonlinearity
Guo-Bao Zhang, Ruyun Ma
Abstract:
This article concerns the bistable traveling wavefronts of a
nonlocal dispersal equation with convolution type bistable
nonlinearity. Applying a homotopy method, we establish the existence
of traveling wavefronts. If the wave speed does not vanish, i.e.
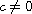 ,
then the uniqueness (up to translation) and the globally
asymptotical stability of traveling wavefronts are proved by the
comparison principle and squeezing technique.
,
then the uniqueness (up to translation) and the globally
asymptotical stability of traveling wavefronts are proved by the
comparison principle and squeezing technique.
Submitted August 8, 2014. Published June 6, 2015.
Math Subject Classifications: 35K57, 35R20, 92D25.
Key Words: Nonlocal dispersal; traveling wavefronts; bistable nonlinearity;
continuation method; squeezing technique.
Show me the PDF file (349 KB),
TEX file, and other files for this article.
 |
Guo-Bao Zhang
College of Mathematics and Statistics
Northwest Normal University
Lanzhou, Gansu 730070, China
email: zhanggb2011@nwnu.edu.cn
|
|---|
 |
Ruyun Ma
College of Mathematics and Statistics
Northwest Normal University
Lanzhou, Gansu 730070, China
email: mary@nwnu.edu.cn
|
|---|
Return to the EJDE web page
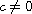 ,
then the uniqueness (up to translation) and the globally
asymptotical stability of traveling wavefronts are proved by the
comparison principle and squeezing technique.
,
then the uniqueness (up to translation) and the globally
asymptotical stability of traveling wavefronts are proved by the
comparison principle and squeezing technique.

