Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 141, pp. 1-24.
Cauchy problems for fifth-order KdV equations in weighted Sobolev spaces
Eddye Bustamante, Jose Jimenez, Jorge Mejia
Abstract:
In this work we study the initial-value problem for the fifth-order
Korteweg-de Vries equation
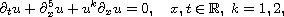
in weighted Sobolev spaces
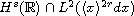 .
We prove local and global results. For the case
.
We prove local and global results. For the case
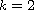 we point out the
relationship between decay and regularity of solutions of the
initial-value problem.
we point out the
relationship between decay and regularity of solutions of the
initial-value problem.
Submitted March 29, 2015. Published May 21, 2015.
Math Subject Classifications: 35Q53, 37K05.
Key Words: Nonlinear dispersive equations; weighted Sobolev spaces.
Show me the PDF file (349 KB),
TEX file, and other files for this article.
 |
Eddye Bustamante M.
Departamento de Matemáticas
Universidad Nacional de Colombia
A. A. 3840 Medellín, Colombia
email: eabusta0@unal.edu.co
|
|---|
 |
José Jiménez U.
Departamento de Matemáticas
Universidad Nacional de Colombia
A. A. 3840 Medellín, Colombia
email: jmjimene@unal.edu.co
|
|---|
 |
Jorge Mejía L.
Departamento de Matemáticas
Universidad Nacional de Colombia
A. A. 3840 Medellín, Colombia
email: jemejia@unal.edu.co
|
|---|
Return to the EJDE web page
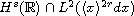 .
We prove local and global results. For the case
.
We prove local and global results. For the case
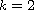 we point out the
relationship between decay and regularity of solutions of the
initial-value problem.
we point out the
relationship between decay and regularity of solutions of the
initial-value problem.


