Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 125, pp. 1-10.
Existence and multiplicity of solutions for sublinear
ordinary differential equations at resonance
Chengyue Li, Fenfen Chen
Abstract:
Using a
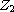 type index theorem, we show the existence and multiplicity
of solutions for the sublinear ordinary differential equation
type index theorem, we show the existence and multiplicity
of solutions for the sublinear ordinary differential equation

with suitable periodic or boundary conditions.
Here
 is a linear positive selfadjoint operator,
is a linear positive selfadjoint operator,
 is a parameter between two egienvalues of this operator,
and
is a parameter between two egienvalues of this operator,
and
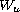 is the gradient of a potential function.
is the gradient of a potential function.
Submitted February 5, 2015. Published May 6, 2015.
Math Subject Classifications: 58E05, 34C37, 70H05.
Key Words: Sublinear potential;
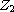 type index theorem;
critical point; resonance; Hamiltonian system.
type index theorem;
critical point; resonance; Hamiltonian system.
Show me the PDF file (235 KB),
TEX file, and other files for this article.
 |
Chengyue Li
Department of Mathematics
Minzu University of China
Beijing 100081, China
email: cunlcy@163.com
|
|---|
 |
Fenfen Chen
Department of Mathematics
Minzu University of China
Beijing 100081, China
email: chenfenfen359@163.com
|
|---|
Return to the EJDE web page
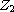 type index theorem, we show the existence and multiplicity
of solutions for the sublinear ordinary differential equation
type index theorem, we show the existence and multiplicity
of solutions for the sublinear ordinary differential equation

 is a linear positive selfadjoint operator,
is a linear positive selfadjoint operator,
 is a parameter between two egienvalues of this operator,
and
is a parameter between two egienvalues of this operator,
and
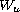 is the gradient of a potential function.
is the gradient of a potential function.

