In this work we prove the existence of infinitely many nonradial solutions, that change sign, to the problem
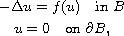
where B is the unit ball in
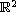 and f
is a continuous and odd function with critical exponential growth.
and f
is a continuous and odd function with critical exponential growth.
Denilson S. Pereira
Abstract:
In this work we prove the existence of infinitely many nonradial solutions,
that change sign, to the problem
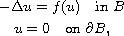
where B is the unit ball in
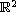 and f
is a continuous and odd function with critical exponential growth.
and f
is a continuous and odd function with critical exponential growth.
Submitted January 29, 2015. Published April 30, 2015.
Math Subject Classifications: 35A15, 35J15.
Key Words: Variational method; critical exponential growth;
sign-changing solution.
Show me the PDF file (357 KB), TEX file, and other files for this article.
 |
Denilson S. Pereira Universidade Federal de Campina Grande Unidade Acadêmica de Matemética - UAMat CEP: 58.429-900 - Campina Grande - PB, Brazil email: denilsonsp@dme.ufcg.edu.br |
|---|
Return to the EJDE web page