Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 118, pp. 1-11.
Positive ground state solutions to Schrodinger-Poisson systems
with a negative non-local term
Yan-Ping Gao, Sheng-Long Yu, Chun-Lei Tang
Abstract:
In this article, we study the Schrodinger-Poisson system
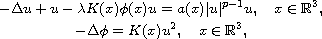
with
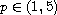 . Assume that
. Assume that
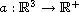 and
and
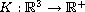 are nonnegative functions and satisfy
suitable assumptions, but not requiring any symmetry property on them,
we prove the existence of a positive ground state solution resolved
by the variational methods.
are nonnegative functions and satisfy
suitable assumptions, but not requiring any symmetry property on them,
we prove the existence of a positive ground state solution resolved
by the variational methods.
Submitted January 20, 2015. Published April 30, 2015.
Math Subject Classifications: 35J47, 35J50, 35J99.
Key Words: Schrodinger-Poisson system; ground state solution;
variational methods.
Show me the PDF file (236 KB),
TEX file, and other files for this article.
 |
Yan-Ping Gao
School of Mathematics and Statistics
Southwest University
Chongqing 400715, China
email: gao0807@swu.edu.cn
|
|---|
 |
Sheng-Long Yu
School of Mathematics and Statistics
Southwest University
Chongqing 400715, China
email: ysl345827434@163.com
|
|---|
 |
Chun-Lei Tang
School of Mathematics and Statistics
Southwest University
Chongqing 400715, China
Phone +86 23 68253135, Fax +86 23 68253135
email: tangcl@swu.edu.cn
|
|---|
Return to the EJDE web page
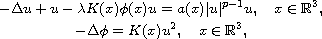
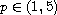 . Assume that
. Assume that
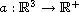 and
and
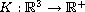 are nonnegative functions and satisfy
suitable assumptions, but not requiring any symmetry property on them,
we prove the existence of a positive ground state solution resolved
by the variational methods.
are nonnegative functions and satisfy
suitable assumptions, but not requiring any symmetry property on them,
we prove the existence of a positive ground state solution resolved
by the variational methods.


