Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 108, pp. 1-17.
Limit cycles for piecewise smooth perturbations of
a cubic polynomial differential center
Shimin Li, Tiren Huang
Abstract:
In this article, we study the planar cubic polynomial differential system
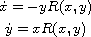
where
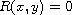 is a conic and
is a conic and
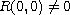 .
We find a bound for the number of limit cycles which bifurcate
from the period annulus of the center, under piecewise
smooth cubic polynomial perturbations.
Our results show that the piecewise smooth cubic system can have at
least 1 more limit cycle than the smooth one.
.
We find a bound for the number of limit cycles which bifurcate
from the period annulus of the center, under piecewise
smooth cubic polynomial perturbations.
Our results show that the piecewise smooth cubic system can have at
least 1 more limit cycle than the smooth one.
Submitted October 24, 2014. Published April 21, 2015.
Math Subject Classifications: 34A36, 34C07, 37G15.
Key Words: Limit cycle; piecewise smooth system; averaging method.
Show me the PDF file (272 KB),
TEX file, and other files for this article.
 |
Shimin Li
School of Mathematics and Statistics
Guangdong University of Finance and Economics
Guangzhou 510320, China
email: lism1983@126.com
|
|---|
 |
Tiren Huang
Department of Mathematics
Zhejiang Sci-Tech University
Hangzhou 310018, China
email: htiren@zstu.edu.cn
|
|---|
Return to the EJDE web page
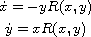
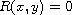 is a conic and
is a conic and
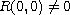 .
We find a bound for the number of limit cycles which bifurcate
from the period annulus of the center, under piecewise
smooth cubic polynomial perturbations.
Our results show that the piecewise smooth cubic system can have at
least 1 more limit cycle than the smooth one.
.
We find a bound for the number of limit cycles which bifurcate
from the period annulus of the center, under piecewise
smooth cubic polynomial perturbations.
Our results show that the piecewise smooth cubic system can have at
least 1 more limit cycle than the smooth one.

