Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 107, pp. 1-13.
Measure integral inclusions with fast oscillating data
Bianca-Renata Satco
Abstract:
We prove the existence of regulated or bounded variation solutions,
via a nonlinear alternative of Leray-Schauder type, for the measure
integral inclusion
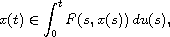
under the assumptions of regularity, respectively bounded variation,
on the function u. Our approach is based on the properties of
Kurzweil-Stieltjes integral that, unlike the classical integrals,
can be used for fast oscillating multifunctions on the right hand
side and the results allow one to study (by taking the function u
of a particular form) continuous or discrete problems, as well as
impulsive or retarded problems.
Submitted April 29, 2014. Published April 21, 2015.
Math Subject Classifications: 34A60, 93C30, 26A42, 26A39.
Key Words: Measure integral inclusion; Kurzweil-Stieltjes integral;
regulated function; bounded variation.
Show me the PDF file (243 KB),
TEX file, and other files for this article.
Bianca-Renata Satco
Stefan cel Mare University
Faculty of Electrical Engineering and Computer Science
Universitatii 13 - 720229 Suceava, Romania
email: bianca.satco@eed.usv.ro Phone/Fax: +40 230 524 801
|
Return to the EJDE web page