Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 102, pp. 1-12.
Existence and multiplicity of solutions for nonhomogeneous
Klein-Gordon-Maxwell equations
Liping Xu, Haibo Chen
Abstract:
This article concerns the nonhomogeneous Klein-Gordon-Maxwell equation
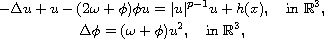
where
 is constant,
is constant,
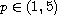 .
Under appropriate assumptions
on h(x), the existence of at least two solutions is obtained by applying
the Ekeland's variational principle and the Mountain Pass Theorem in
critical point theory.
.
Under appropriate assumptions
on h(x), the existence of at least two solutions is obtained by applying
the Ekeland's variational principle and the Mountain Pass Theorem in
critical point theory.
Submitted January 21, 2015. Published April 16, 2015.
Math Subject Classifications: 35J20, 35J65, 35J60.
Key Words: Nonhomogeneous Klein-Gordon-Maxwell equations; multiple solutions;
Pohozaev identity; variational method.
Show me the PDF file (253 KB),
TEX file, and other files for this article.
 |
Liping Xu
School of Mathematics and Statistics
Central South University
Changsha 410075, China
email: x.liping@126.com
|
|---|
 |
Haibo Chen
School of Mathematics and Statistics
Central South University
Changsha 410075, China
email: math_chb@csu.edu.cn
|
|---|
Return to the EJDE web page
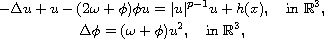
 is constant,
is constant,
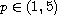 .
Under appropriate assumptions
on h(x), the existence of at least two solutions is obtained by applying
the Ekeland's variational principle and the Mountain Pass Theorem in
critical point theory.
.
Under appropriate assumptions
on h(x), the existence of at least two solutions is obtained by applying
the Ekeland's variational principle and the Mountain Pass Theorem in
critical point theory.

