Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 09, pp. 1-10.
Particular solutions of generalized Euler-Poisson-Darboux equation
Rakhila B. Seilkhanova, Anvar H. Hasanov
Abstract:
In this article we consider the generalized Euler-Poisson-Darboux equation
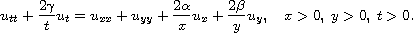
We construct particular solutions in an explicit form expressed by
the Lauricella hypergeometric function of three variables.
Properties of each constructed solutions have been investigated in sections
of surfaces of the characteristic cone. Precisely, we prove that found
solutions have singularity
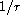 at
at
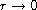 ,
where
,
where
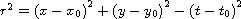 .
.
Submitted October 21, 2014. Published January 5, 2015.
Math Subject Classifications: 35Q05, 35L80, 35C65.
Key Words: Generalized Euler-Poisson-Darboux equation;
hyperbolic equation; Lauricelli hypergeometric functions.
Show me the PDF file (207 KB),
TEX file, and other files for this article.
 |
Rakhila B. Seilkhanova
S. Baishev University Aktobe
Department for Information Systems and Applied Mathematics
030000 Aktobe, Zhubanov str. 302, Kazakhstan
email: srahila@inbox.ru
|
|---|
 |
Anvar H. Hasanov
S. Baishev University Aktobe
Department for Information Systems and Applied Mathematics
030000 Aktobe, Zhubanov str. 302, Kazakhstan
email: anvarhasanov@yahoo.com
|
|---|
Return to the EJDE web page
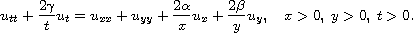
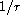 at
at
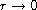 ,
where
,
where
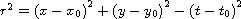 .
.

