Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 07, pp. 1-17.
Local well-posedness and blow-up of solutions for wave equations
on shallow water with periodic depth
Lili Fan, Hongjun Gao
Abstract:
In this article, we consider a nonlinear evolution equation for surface
waves in shallow water over periodic uneven bottom. The local well-posedness
in Sobolev space
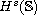 with
with
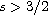 is established by
applying Kato's theory. Then a blow up criterion is determined in
is established by
applying Kato's theory. Then a blow up criterion is determined in
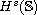 ,
,
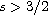 .
Finally, some blow-up results are given for
a simplified model.
.
Finally, some blow-up results are given for
a simplified model.
Submitted September 24, 2014. Published January 5, 2015.
Math Subject Classifications: 35Q53, 35B30, 35G25, 35B44.
Key Words: Shallow water equation; variable depth; well-posedness; blow-up.
Show me the PDF file (284 KB),
TEX file, and other files for this article.
Lili Fan
School of Mathematical Science and Jiangsu Key Laboratory for NSLSCS
Nanjing Normal University, Nanjing 210023, China
email: fanlily89@126.com
|
Hongjun Gao
School of Mathematical Science and Jiangsu Key Laboratory for NSLSCS
Nanjing Normal University, Nanjing 210023, China.
email: gaohj@njnu.edu.cn
|
Return to the EJDE web page
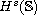 with
with
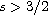 is established by
applying Kato's theory. Then a blow up criterion is determined in
is established by
applying Kato's theory. Then a blow up criterion is determined in
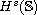 ,
,
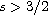 .
Finally, some blow-up results are given for
a simplified model.
.
Finally, some blow-up results are given for
a simplified model.