Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 03, pp. 1-9.
Existence and concentration of solutions for sublinear fourth-order
elliptic equations
Wen Zhang, Xianhua Tang, Jian Zhang
Abstract:
This article concerns the fourth-order elliptic equations
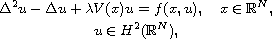
where
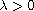 is a parameter,
is a parameter,
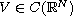 and
and
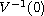 has nonempty interior. Under some mild assumptions, we establish the existence
of nontrivial solutions. Moreover, the concentration of solutions is also
explored on the set
has nonempty interior. Under some mild assumptions, we establish the existence
of nontrivial solutions. Moreover, the concentration of solutions is also
explored on the set
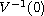 as
as
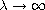 .
.
Submitted November 23, 2014. Published January 5, 2015.
Math Subject Classifications: 35J35, 35J60.
Key Words: Fourth-order elliptic equations; variational method; concentration.
Show me the PDF file (228 KB),
TEX file, and other files for this article.
 |
Wen Zhang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: zwmath2011@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Jian Zhang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: zhangjian433130@163.com
|
|---|
Return to the EJDE web page
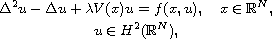
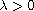 is a parameter,
is a parameter,
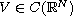 and
and
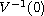 has nonempty interior. Under some mild assumptions, we establish the existence
of nontrivial solutions. Moreover, the concentration of solutions is also
explored on the set
has nonempty interior. Under some mild assumptions, we establish the existence
of nontrivial solutions. Moreover, the concentration of solutions is also
explored on the set
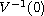 as
as
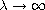 .
.


