Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 93, pp. 1-14.
Existence and multiplicity of positive periodic
solutions for second-order functional differential
equations with infinite delay
Qiang Li, Yongxiang Li
Abstract:
In this article, the existence and multiplicity results of positive
periodic solutions are obtained for the second-order functional
differential equation with infinite delay

where
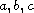 are continuous
are continuous
 -periodic
functions,
-periodic
functions,
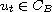 is defined by
is defined by
 for
for
![$s\in(-\infty,0]$](gifs/af.gif) ,
,
 denotes the Banach space of bounded continuous function
denotes the Banach space of bounded continuous function
![$\phi:(-\infty,0]\to\mathbb{R}$](gifs/ah.gif) with the norm
with the norm
![$\|\phi\|_B=\sup_{s\in(-\infty,0]}|\phi(s)|$](gifs/ai.gif) ,
and
,
and
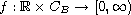 is a nonnegative continuous functional.
The existence conditions concern with the first eigenvalue of the associated
linear periodic boundary problem. Our discussion is based on the fixed point
index theory in cones.
is a nonnegative continuous functional.
The existence conditions concern with the first eigenvalue of the associated
linear periodic boundary problem. Our discussion is based on the fixed point
index theory in cones.
Submitted September 22, 2013. Published April 4, 2014.
Math Subject Classifications: 34C25, 47H10.
Key Words: Second-order functional differential equations; first eigenvalue;
positive periodic solution; cone; fixed point index.
Show me the PDF file (272 KB),
TEX file, and other files for this article.
 |
Qiang Li
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: lznwnuliqiang@126.com
|
|---|
 |
Yongxiang Li
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: liyxnwnu@163.com, Phone 86-0931-7971111
|
|---|
Return to the EJDE web page

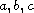 are continuous
are continuous
 -periodic
functions,
-periodic
functions,
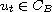 is defined by
is defined by
 for
for
![$s\in(-\infty,0]$](gifs/af.gif) ,
,
 denotes the Banach space of bounded continuous function
denotes the Banach space of bounded continuous function
![$\phi:(-\infty,0]\to\mathbb{R}$](gifs/ah.gif) with the norm
with the norm
![$\|\phi\|_B=\sup_{s\in(-\infty,0]}|\phi(s)|$](gifs/ai.gif) ,
and
,
and
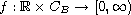 is a nonnegative continuous functional.
The existence conditions concern with the first eigenvalue of the associated
linear periodic boundary problem. Our discussion is based on the fixed point
index theory in cones.
is a nonnegative continuous functional.
The existence conditions concern with the first eigenvalue of the associated
linear periodic boundary problem. Our discussion is based on the fixed point
index theory in cones.

