Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 91, pp. 1-16.
Weighted asymptotic behavior of solutions to semilinear
integro-differential equations in Banach spaces
Yan-Tao Bian, Yong-Kui Chang, Juan J. Nieto
Abstract:
In this article, we study weighted asymptotic behavior of solutions to
the semilinear integro-differential equation
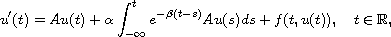
where
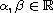 ,
with
,
with
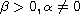 and
and
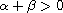 ,
A is the generator of an immediately norm continuous
,
A is the generator of an immediately norm continuous
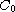 -Semigroup
defined on a Banach space
-Semigroup
defined on a Banach space
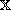 ,
and
,
and
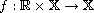 is an
is an
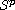 -weighted
pseudo almost automorphic function satisfying suitable conditions.
Some sufficient conditions are established by using properties of
-weighted
pseudo almost automorphic function satisfying suitable conditions.
Some sufficient conditions are established by using properties of
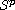 -weighted
pseudo almost automorphic functions combined with
theories of uniformly exponentially stable and strongly continuous family
of operators.
-weighted
pseudo almost automorphic functions combined with
theories of uniformly exponentially stable and strongly continuous family
of operators.
Submitted October 21, 2013. Published April 2, 2014.
Math Subject Classifications: 4K14, 60H10, 35B15, 34F05.
Key Words: Integro-differential equations; uniformly exponentially stable;
Stepanov-like weighted pseudo almost automorphy.
Show me the PDF file (296 KB),
TEX file, and other files for this article.
 |
Yan-Tao Bian
Department of Mathematics,
Lanzhou Jiaotong University
Lanzhou 730070, China
email: 1120689525@qq.com
|
|---|
 |
Yong-Kui Chang
Department of Mathematics, Lanzhou Jiaotong University
Lanzhou 730070, China
email: lzchangyk@163.com
|
|---|
 |
Juan J. Nieto
Departamento de Análisis Matemático,
Facultad de Matemáticas
Universidad de Santiago de Compostela
15782, Santiago de Compostela, Spain
email: juanjose.nieto.roig@usc.es
|
|---|
Return to the EJDE web page
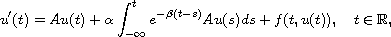
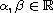 ,
with
,
with
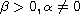 and
and
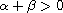 ,
A is the generator of an immediately norm continuous
,
A is the generator of an immediately norm continuous
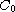 -Semigroup
defined on a Banach space
-Semigroup
defined on a Banach space
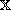 ,
and
,
and
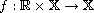 is an
is an
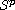 -weighted
pseudo almost automorphic function satisfying suitable conditions.
Some sufficient conditions are established by using properties of
-weighted
pseudo almost automorphic function satisfying suitable conditions.
Some sufficient conditions are established by using properties of
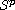 -weighted
pseudo almost automorphic functions combined with
theories of uniformly exponentially stable and strongly continuous family
of operators.
-weighted
pseudo almost automorphic functions combined with
theories of uniformly exponentially stable and strongly continuous family
of operators.


