Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 90, pp. 1-15.
Self-similar solutions with compactly supported profile of some
nonlinear Schrodinger equations
Pascal Begout, Jesus Ildefonso Diaz
Abstract:
``Sharp localized'' solutions (i.e. with compact support for each given time t)
of a singular nonlinear type Schr\"odinger equation in the whole space
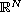 are constructed here under the assumption that they have
a self-similar structure. It requires the assumption that the external
forcing term satisfies that
are constructed here under the assumption that they have
a self-similar structure. It requires the assumption that the external
forcing term satisfies that
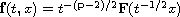 for some complex exponent
for some complex exponent
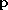 and for some profile function
and for some profile function
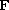 which is assumed to be with compact support in
which is assumed to be with compact support in
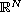 .
We show the existence of solutions of the form
.
We show the existence of solutions of the form
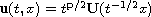 ,
with a profile
,
with a profile
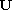 ,
which also has compact support in
,
which also has compact support in
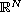 .
The proof of the localization of the support of the profile
.
The proof of the localization of the support of the profile
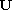 uses some suitable energy method applied to the stationary problem satisfied
by
uses some suitable energy method applied to the stationary problem satisfied
by
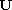 after some unknown transformation.
after some unknown transformation.
Submitted December 9, 2013. Published April 2, 2014.
Math Subject Classifications: 35B99, 35A01, 35A02, 35B65, 35J60.
Key Words: Nonlinear self-similar Schrodinger equation; compact support;
energy method.
Show me the PDF file (283 KB),
TEX file, and other files for this article.
 |
Pascal Bégout
Institut de Mathématiques de Toulouse & TSE
Université Toulouse I Capitole,
Manufacture des Tabacs
21, Allée de Brienne,
31015 Toulouse Cedex 6, France
email: Pascal.Begout@math.cnrs.fr
|
|---|
 |
Jesús Ildefonso Díaz
Departamento de Matemática Aplicada
Instituto de Matemática Interdisciplinar
Universidad Complutense de Madrid
Plaza de las Ciencias, 3, 28040 Madrid, Spain
email: diaz.racefyn@insde.es
|
|---|
Return to the EJDE web page
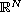 are constructed here under the assumption that they have
a self-similar structure. It requires the assumption that the external
forcing term satisfies that
are constructed here under the assumption that they have
a self-similar structure. It requires the assumption that the external
forcing term satisfies that
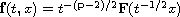 for some complex exponent
for some complex exponent
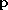 and for some profile function
and for some profile function
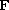 which is assumed to be with compact support in
which is assumed to be with compact support in
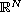 .
We show the existence of solutions of the form
.
We show the existence of solutions of the form
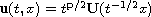 ,
with a profile
,
with a profile
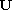 ,
which also has compact support in
,
which also has compact support in
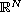 .
The proof of the localization of the support of the profile
.
The proof of the localization of the support of the profile
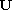 uses some suitable energy method applied to the stationary problem satisfied
by
uses some suitable energy method applied to the stationary problem satisfied
by
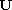 after some unknown transformation.
after some unknown transformation.

