Electron. J. Diff. Equ., Vol. 2014 (2014), No. 89, pp. 1-10.

Hamiltonians representing equations of motion with damping due to friction

Stephen Montgomery-Smith

Abstract:
Suppose that 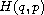$H(q,p)$ is a Hamiltonian on a manifold M, and 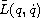$\tilde L(q,\dot q)$, the Rayleigh dissipation function, satisfies the same hypotheses as a Lagrangian on the manifold M. We provide a Hamiltonian framework that gives the equation
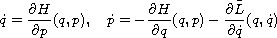
$$ \dot q = \frac{\partial H}{\partial p}(q,p) , \quad \dot p = - \frac{\partial H}{\partial q}(q,p) - \frac{\partial \tilde L}{\partial \dot q}(q,\dot q) $$
The method is to embed M into a larger framework where the motion drives a wave equation on the negative half line, where the energy in the wave represents heat being carried away from the motion. We obtain a version of Nother's Theorem that is valid for dissipative systems. We also show that this framework fits the widely held view of how Hamiltonian dynamics can lead to the ``arrow of time.''

Submitted January 23, 2014. Published April 2, 2014.
Math Subject Classifications: 70H25.
Key Words: Hamiltonian; Lagrangian; Rayleigh dissipation function; friction; Nother's Theorem.

Show me the PDF file (194 KB), TEX file, and other files for this article.

Stephen Montgomery-Smith
Department of Mathematics, University of Missouri
Columbia, MO 65211, USA
email: stephen@missouri.edu

Return to the EJDE web page