Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 86, pp. 1-12.
Existence of solutions to nonlocal Kirchhoff equations
of elliptic type via genus theory
Nemat Nyamoradi, Nguyen Thanh Chung
Abstract:
In this article, we study the existence and multiplicity of
solutions to the nonlocal Kirchhoff fractional equation
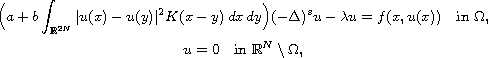
where
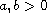 are constants,
are constants,
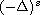 is the fractional
Laplace operator,
is the fractional
Laplace operator,
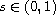 is a fixed real
number,
is a fixed real
number,
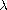 is a real parameter and
is a real parameter and
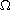 is an open bounded subset
of
is an open bounded subset
of
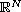 ,
,
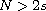 ,
with Lipschitz boundary,
,
with Lipschitz boundary,
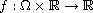 is a continuous function.
The proofs rely essentially on the genus properties in critical point theory.
is a continuous function.
The proofs rely essentially on the genus properties in critical point theory.
Submitted December 15, 2013. Published April 2, 2014.
Math Subject Classifications: 34B27, 35J60, 35B05.
Key Words: Kirchhoff nonlocal operators; fractional differential equations;
genus properties; critical point theory.
Show me the PDF file (267 KB),
TEX file, and other files for this article.
 |
Nemat Nyamoradi
Department of Mathematics, Faculty of Sciences
Razi University, 67149 Kermanshah, Iran
email: nyamoradi@razi.ac.ir, neamat80@yahoo.com
|
|---|
 |
Nguyen Thanh Chung
Department of Mathematics, Quang Binh University
312 Ly Thuong Kiet, Dong Hoi, Quang Binh, Vietnam
email: ntchung82@yahoo.com
|
|---|
Return to the EJDE web page
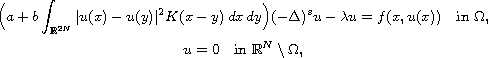
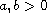 are constants,
are constants,
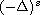 is the fractional
Laplace operator,
is the fractional
Laplace operator,
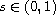 is a fixed real
number,
is a fixed real
number,
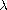 is a real parameter and
is a real parameter and
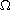 is an open bounded subset
of
is an open bounded subset
of
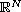 ,
,
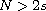 ,
with Lipschitz boundary,
,
with Lipschitz boundary,
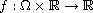 is a continuous function.
The proofs rely essentially on the genus properties in critical point theory.
is a continuous function.
The proofs rely essentially on the genus properties in critical point theory.

