We present a direct algebraic method for obtaining the matrix exponential function exp(tA), expressed as an explicit function of t for any square matrix A whose eigenvalues are known. The explicit form can be used to determine how a given eigenvalue affects the behavior of exp(tA). We use an algebraic convolution formula for basic exponential polynomials to obtain the dynamic solution g(t) associated with the characteristic (or minimal) polynomial w(x) of A. Then exp(tA) is expressed as
,
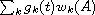where the
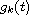are successive derivatives of g and the
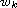are the
Horner polynomials associated with w(x).
Our method also gives a number
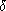that measures how well the computed
approximation satisfies the matrix differential equation
F'(tA)=A F(tA) at some given point
.
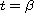Some numerical experiments with random matrices indicate that the proposed
method can be applied to matrices of order up to 40.
