Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 74, pp. 1-11.
Pullback attractor for non-autonomous p-Laplacian
equations with dynamic flux boundary conditions
Bo You, Fang Li
Abstract:
This article studies the long-time asymptotic behavior of solutions for
the non-autonomous
 -Laplacian equation
-Laplacian equation
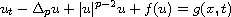
with dynamic flux boundary conditions
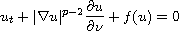
in a n-dimensional bounded smooth domain
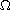 under some
suitable assumptions. We prove the existence of a pullback
attractor in
under some
suitable assumptions. We prove the existence of a pullback
attractor in
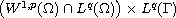 by asymptotic a priori estimate.
by asymptotic a priori estimate.
Submitted June 26, 2013. Published March 18, 2014.
Math Subject Classifications: 35B40, 37B55.
Key Words: Pullback attractor; Sobolev compactness embedding;
p-Laplacian; norm-to-weak continuous process;
asymptotic a priori estimate; non-autonomous;
nonlinear flux boundary conditions.
Show me the PDF file (251 KB),
TEX file, and other files for this article.
Bo You
School of Mathematics and Statistics
Xi'an Jiaotong University
Xi'an, 710049, China
email: youb03@126.com
|
Fang Li
Department of Mathematics, Nanjing University
Nanjing, 210093, China
email: lifang101216@126.com
|
Return to the EJDE web page
 -Laplacian equation
-Laplacian equation
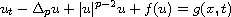
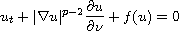
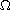 under some
suitable assumptions. We prove the existence of a pullback
attractor in
under some
suitable assumptions. We prove the existence of a pullback
attractor in
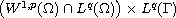 by asymptotic a priori estimate.
by asymptotic a priori estimate.