Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 61, pp. 1-14.
Solutions to third-order multi-point boundary-value problems
at resonance with three dimensional kernels
Shuang Li, Jian Yin, Zengji Du
Abstract:
In this article, we consider the boundary-value problem
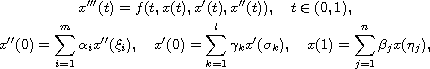
where
![$f: [0, 1]\times \mathbb{R}^3\to \mathbb{R}$](gifs/ab.gif) is a Caratheodory
function, and the kernel to the linear operator has dimension three.
Under some resonance conditions, by using the coincidence
degree theorem, we show the existence of solutions. An example
is given to illustrate our results.
is a Caratheodory
function, and the kernel to the linear operator has dimension three.
Under some resonance conditions, by using the coincidence
degree theorem, we show the existence of solutions. An example
is given to illustrate our results.
Submitted October 13, 2013. Published March 5, 2014.
Math Subject Classifications: 34B15.
Key Words: Multi-point boundary-value problem; coincidence degree theory;
resonance.
Show me the PDF file (243 KB),
TEX file, and other files for this article.
 |
Shuang Li
School of Management
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: lishuangchina@163.com
|
|---|
 |
Jian Yin
School of Mathematics and Statistics
Jiangsu Normal University
Xuzhou, Jiangsu 221116, China
email: yinjian719@163.com
|
|---|
 |
Zengji Du
School of Mathematics and Statistics
Jiangsu Normal University
Xuzhou, Jiangsu 221116, China
email: duzengji@163.com, Fax 0086-516-83403299
|
|---|
Return to the EJDE web page
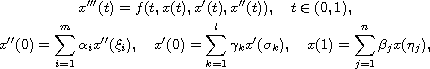
![$f: [0, 1]\times \mathbb{R}^3\to \mathbb{R}$](gifs/ab.gif) is a Caratheodory
function, and the kernel to the linear operator has dimension three.
Under some resonance conditions, by using the coincidence
degree theorem, we show the existence of solutions. An example
is given to illustrate our results.
is a Caratheodory
function, and the kernel to the linear operator has dimension three.
Under some resonance conditions, by using the coincidence
degree theorem, we show the existence of solutions. An example
is given to illustrate our results.


