Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 58, pp. 1-10.
Solvability of fractional multi-point boundary-value problems with
p-Laplacian operator at resonance
Tengfei Shen, Wenbin Liu, Taiyong Chen, Xiaohui Shen
Abstract:
In this article, we consider the multi-point boundary-value problem
for nonlinear fractional differential equations with
 -Laplacian operator:
-Laplacian operator:
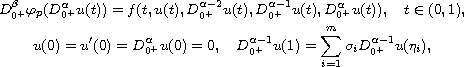
where
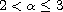 ,
,
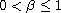 ,
,
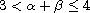 ,
,
 ,
,
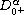 is the standard
Riemann-Liouville fractional derivative.
is the standard
Riemann-Liouville fractional derivative.
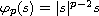 is
p-Laplacians operator. The existence of solutions for above fractional
boundary value problem is obtained by using the extension of Mawhin's
continuation theorem due to Ge, which enrich konwn results.
An example is given to illustrate the main result.
is
p-Laplacians operator. The existence of solutions for above fractional
boundary value problem is obtained by using the extension of Mawhin's
continuation theorem due to Ge, which enrich konwn results.
An example is given to illustrate the main result.
Submitted January 13, 2013. Published February 28, 2014.
Math Subject Classifications: 34A08, 34B15.
Key Words: Fractional differential equation; boundary value problem;
p-Laplacian operator; Coincidence degree theory; Resonance.
Show me the PDF file (231 KB),
TEX file, and other files for this article.
 |
Tengfei Shen
College of Sciences
China University of Mining and Technology
Xuzhou 221008, China
email: shentengfei1987@126.com
|
|---|
 |
Wenbin Liu
College of Sciences
China University of Mining and Technology
Xuzhou 221008, China
email: wblium@163.com
|
|---|
 |
Taiyong Chen
College of Sciences
China University of Mining and Technology
Xuzhou 221008, China
email: taiyongchen@cumt.edu.cn
|
|---|
 |
Xiaohui Shen
College of Sciences
China University of Mining and Technology
Xuzhou 221008, China
email: shenxiaohuicool@163.com
|
|---|
Return to the EJDE web page
 -Laplacian operator:
-Laplacian operator:
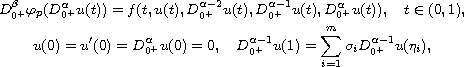
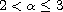 ,
,
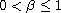 ,
,
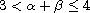 ,
,
 ,
,
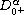 is the standard
Riemann-Liouville fractional derivative.
is the standard
Riemann-Liouville fractional derivative.
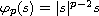 is
p-Laplacians operator. The existence of solutions for above fractional
boundary value problem is obtained by using the extension of Mawhin's
continuation theorem due to Ge, which enrich konwn results.
An example is given to illustrate the main result.
is
p-Laplacians operator. The existence of solutions for above fractional
boundary value problem is obtained by using the extension of Mawhin's
continuation theorem due to Ge, which enrich konwn results.
An example is given to illustrate the main result.



