Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 45, pp. 1-11.
Asymptotic behavior of singular solutions to semilinear
fractional elliptic equations
Guowei Lin, Xiongjun Zheng
Abstract:
In this article we study the asymptotic behavior of positive singular
solutions to the equation
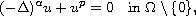
subject to the conditions
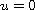 in
in
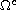 and
and
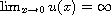 ,
where
,
where
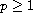 ,
,
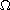 is an open bounded regular domain in
is an open bounded regular domain in
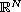 (
(
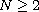 )
containing the origin, and
)
containing the origin, and
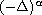 with
with
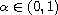 denotes the fractional Laplacian.
We show that the asymptotic behavior of positive singular solutions
is controlled by a radially symmetric solution with
denotes the fractional Laplacian.
We show that the asymptotic behavior of positive singular solutions
is controlled by a radially symmetric solution with
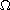 being a ball.
being a ball.
Submitted September 24, 2013. Published February 10, 2014.
Math Subject Classifications: 35R11, 35B06, 35B40.
Key Words: Fractional Laplacian; radial symmetry;
asymptotic behavior; singular solution.
Show me the PDF file (251 KB),
TEX file, and other files for this article.
 |
Guowei Lin
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: lgw2008@sina.cn
|
|---|
 |
Xiongjun Zheng
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: xjzh1985@126.com
|
|---|
Return to the EJDE web page
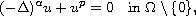
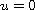 in
in
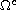 and
and
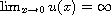 ,
where
,
where
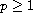 ,
,
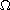 is an open bounded regular domain in
is an open bounded regular domain in
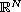 (
(
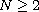 )
containing the origin, and
)
containing the origin, and
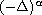 with
with
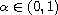 denotes the fractional Laplacian.
We show that the asymptotic behavior of positive singular solutions
is controlled by a radially symmetric solution with
denotes the fractional Laplacian.
We show that the asymptotic behavior of positive singular solutions
is controlled by a radially symmetric solution with
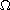 being a ball.
being a ball.

