Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 37, pp. 1-10.
Existence of positive solutions for p-Laplacian an
m-point boundary value problem involving the derivative on time scales
Abdulkadir Dogan
Abstract:
We are interested in the existence of positive solutions for the -Laplacian
dynamic equation on time scales,
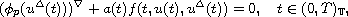
subject to the multipoint boundary condition,

where
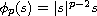 ,
,
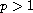 ,
,
![$\xi_i\in [0,T]_{\mathbb{T}}$](gifs/ae.gif) ,
,
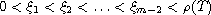 .
By using fixed point theorems, we prove the existence of at least three
non-negatvie solutions, two of them positive, to the above boundary value
problem. The interesting point is the nonlinear term f is involved with
the first order derivative explicitly.
An example is given to illustrate the main result.
.
By using fixed point theorems, we prove the existence of at least three
non-negatvie solutions, two of them positive, to the above boundary value
problem. The interesting point is the nonlinear term f is involved with
the first order derivative explicitly.
An example is given to illustrate the main result.
Submitted December 3, 2013. Published January 30, 2014.
Math Subject Classifications: 34B15, 34B16, 34B18, 39A10.
Key Words: Time scales; boundary value problem; p-Laplacian;
positive solution; fixed point theorem.
Show me the PDF file (228 KB),
TEX file, and other files for this article.
 |
Abdulkadir Dogan
Department of Applied Mathematics
Faculty of Computer Sciences
Abdullah Gul University, Kayseri, 38039 Turkey
Tel: +90 352 224 88 00 Fax: +90 352 338 88 28
email: abdulkadir.dogan@agu.edu.tr
|
|---|
Return to the EJDE web page
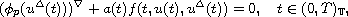

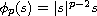 ,
,
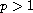 ,
,
![$\xi_i\in [0,T]_{\mathbb{T}}$](gifs/ae.gif) ,
,
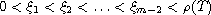 .
By using fixed point theorems, we prove the existence of at least three
non-negatvie solutions, two of them positive, to the above boundary value
problem. The interesting point is the nonlinear term f is involved with
the first order derivative explicitly.
An example is given to illustrate the main result.
.
By using fixed point theorems, we prove the existence of at least three
non-negatvie solutions, two of them positive, to the above boundary value
problem. The interesting point is the nonlinear term f is involved with
the first order derivative explicitly.
An example is given to illustrate the main result.
