Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 30, pp. 1-10.
Exact number of solutions for a Neumann problem involving the p-Laplacian
Justino Sanchez, Vicente Vergara
Abstract:
We study the exact number of solutions of the quasilinear Neumann
boundary-value problem

where
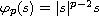 denotes the one-dimensional
p-Laplacian. Under appropriate hypotheses on g and h,
we obtain existence, multiplicity, exactness and
non existence results. The existence of solutions is
proved using the method of upper and lower solutions.
denotes the one-dimensional
p-Laplacian. Under appropriate hypotheses on g and h,
we obtain existence, multiplicity, exactness and
non existence results. The existence of solutions is
proved using the method of upper and lower solutions.
Submitted September 26, 2013. Published January 27, 2014.
Math Subject Classifications: 34B15, 35J60.
Key Words: Neumann boundary value problem; p-Laplacian;
lower-upper solutions; exact multiplicity.
Show me the PDF file (240 KB),
TEX file, and other files for this article.
 |
Justino Sánchez
Departamento de Matemáticas, Universidad de La Serena
Avda. Cisternas 1200, La Serena, Chile
email: jsanchez@userena.cl
|
|---|
 |
Vicente Vergara
Instituto de Alta Investigación, Universidad de Tarapacá
Antofagasta No. 1520, Arica, Chile
email: vvergaraa@uta.cl
|
|---|
Return to the EJDE web page

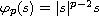 denotes the one-dimensional
p-Laplacian. Under appropriate hypotheses on g and h,
we obtain existence, multiplicity, exactness and
non existence results. The existence of solutions is
proved using the method of upper and lower solutions.
denotes the one-dimensional
p-Laplacian. Under appropriate hypotheses on g and h,
we obtain existence, multiplicity, exactness and
non existence results. The existence of solutions is
proved using the method of upper and lower solutions.

