Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 263, pp. 1-13.
Critical exponent and blow-up rate for the omega-diffusion
equations on graphs with Dirichlet boundary conditions
Weican Zhou, Miaomiao Chen, Wenjun Liu
Abstract:
In this article, we study the
 -diffusion
equation on a graph
with Dirichlet boundary conditions
-diffusion
equation on a graph
with Dirichlet boundary conditions
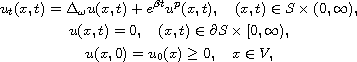
where
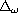 is the discrete weighted Laplacian operator.
First, we prove the existence and uniqueness of the local solution
via Banach fixed point theorem. Then, by the method of supersolutions
and subsolutions we prove that the
is the discrete weighted Laplacian operator.
First, we prove the existence and uniqueness of the local solution
via Banach fixed point theorem. Then, by the method of supersolutions
and subsolutions we prove that the
 -diffusion
problem has a
critical exponent
-diffusion
problem has a
critical exponent
 : when
: when
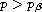 ,
the solution becomes
global; while when
,
the solution becomes
global; while when
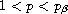 ,
the solution blows up in finite time.
Under appropriate hypotheses, we estimate the blow-up rate in the
,
the solution blows up in finite time.
Under appropriate hypotheses, we estimate the blow-up rate in the
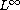 -norm.
Some numerical experiments illustrate our results.
-norm.
Some numerical experiments illustrate our results.
Submitted July 10, 2014. Published December 22, 2014.
Math Subject Classifications: 35R02, 35B44, 35B51.
Key Words: Omega-diffusion equation; critical exponent; blow up;
blow-up rate; graph.
Show me the PDF file (297 KB),
TEX file, and other files for this article.
 |
Weican Zhou
College of Mathematics and Statistics
Nanjing University of Information Science and Technology
Nanjing 210044, China
email: 000496@nuist.edu.cn
|
|---|
 |
Miaomiao Chen
College of Mathematics and Statistics
Nanjing University of Information Science and Technology
Nanjing 210044, China
email: mmchennuist@163.com
|
|---|
 |
Wenjun Liu
College of Mathematics and Statistics
Nanjing University of Information Science and Technology
Nanjing 210044, China
email: wjliu@nuist.edu.cn
|
|---|
Return to the EJDE web page
 -diffusion
equation on a graph
with Dirichlet boundary conditions
-diffusion
equation on a graph
with Dirichlet boundary conditions
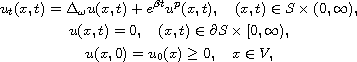
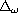 is the discrete weighted Laplacian operator.
First, we prove the existence and uniqueness of the local solution
via Banach fixed point theorem. Then, by the method of supersolutions
and subsolutions we prove that the
is the discrete weighted Laplacian operator.
First, we prove the existence and uniqueness of the local solution
via Banach fixed point theorem. Then, by the method of supersolutions
and subsolutions we prove that the
 -diffusion
problem has a
critical exponent
-diffusion
problem has a
critical exponent
 : when
: when
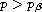 ,
the solution becomes
global; while when
,
the solution becomes
global; while when
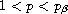 ,
the solution blows up in finite time.
Under appropriate hypotheses, we estimate the blow-up rate in the
,
the solution blows up in finite time.
Under appropriate hypotheses, we estimate the blow-up rate in the
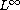 -norm.
Some numerical experiments illustrate our results.
-norm.
Some numerical experiments illustrate our results.


