 -Laplacian eigenvalue problems
-Laplacian eigenvalue problems
 -Laplacian eigenvalue problems
-Laplacian eigenvalue problems
Yan-Hsiou Cheng, Chun-Kong Law, Yu-Chen Luo
Abstract:
The Prufer angle is an effective tool for studying Sturm-Liouville problems
and p-Laplacian eigenvalue problems.
In this article, we show that for the p-Laplacian eigenvalue problem, when
x is irrational in (0,1), a sequence of modified
Prufer angles (after modulo
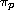 ) is equidistributed
in
) is equidistributed
in
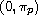 . As a function of x,
. As a function of x,
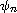 is also asymptotic to
the uniform distribution on
(0,\pi_p).
is also asymptotic to
the uniform distribution on
(0,\pi_p).
Submitted November 11, 2014. Published December 4, 2014.
Math Subject Classifications: 34B24, 37A30
Key Words: p-Laplacian eigenvalue problem; Prufer angle;
equidistribution; uniform distribution.
Show me the PDF file (212 KB), TEX file, and other files for this article.
 |
Yan-Hsiou Cheng Department of Mathematics and Information Education National Taipei University of Education Taipei 106, Taiwan email: yhcheng@tea.ntue.edu.tw |
|---|---|
 |
Chun-Kong Law Department of Applied Mathematics National Sun Yat-sen University Kaohsiung 80424, Taiwan email: law@math.nsysu.edu.tw |
 |
Yu-Chen Luo Department of Applied Mathematics National Sun Yat-sen University Kaohsiung 80424, Taiwan email: leoredro@gmail.com |
Return to the EJDE web page