Electron. J. Diff. Equ., Vol. 2014 (2014), No. 253, pp. 1-13.

Ground states for Schrodinger-Poisson systems with three growth terms

Hui Zhang, Fubao Zhang, Junxiang Xu

Abstract:
In this article we study the existence and nonexistence of ground states of the Schr\"odinger-Poisson system
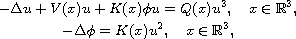
$$\displaylines{ -\Delta u+V(x)u+K(x)\phi u=Q(x)u^3,\quad x\in \mathbb{R}^3,\cr -\Delta\phi=K(x)u^2, \quad x\in \mathbb{R}^3, }$$
where V, K, and Q are asymptotically periodic in the variable x. The proof is based on the the method of Nehari manifold and concentration compactness principle. In particular, we develop the method of Nehari manifold for Schrodinger-Poisson systems with three times growth.

Submitted September 9, 2014. Published December 4, 2014.
Math Subject Classifications: 35J05, 35J50, 35J60.
Key Words: Schrodinger-Poisson system; variational method; ground state; asymptotically periodic.

Show me the PDF file (252 KB), TEX file, and other files for this article.

Hui Zhang
Department of Mathematics
Jinling Institute of Technology
Nanjing 211169, China
email: huihz0517@126.com
  Fubao Zhang
Department of Mathematics, Southeast University
Nanjing 210096, China
email: zhangfubao@seu.edu.cn
  Junxiang Xu
Department of Mathematics, Southeast University
Nanjing 210096, China
email: xujun@seu.edu.cn

Return to the EJDE web page