Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 251, pp. 1-11.
Semiclassical solutions for linearly coupled Schrodinger equations
Sitong Chen, Xianhua Tang
Abstract:
We consider the system of coupled nonlinear Schrodinger equations
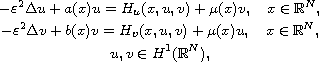
where
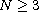 ,
,
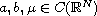 and
and
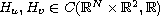 .
Under conditions that
.
Under conditions that
 or
or
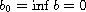 and
and
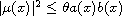 with
with
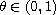 and some mild assumptions on
and some mild assumptions on
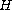 ,
we show that the system has at least one
nontrivial solution provided that
,
we show that the system has at least one
nontrivial solution provided that
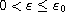 , where the bound
, where the bound
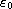 is
formulated in terms of N, a, b and H.
is
formulated in terms of N, a, b and H.
Submitted October 23, 2014. Published December 1, 2014.
Math Subject Classifications: 35J20, 58E50.
Key Words: Nonlinear Schrodinger equation; semiclassical solution; coupled system;
Show me the PDF file (252 KB),
TEX file, and other files for this article.
 |
Sitong Chen
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email:sitongchen2041@hotmail.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: tangxh@mail.csu.edu.cn
|
|---|
Return to the EJDE web page
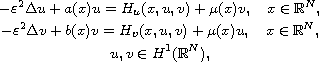
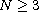 ,
,
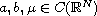 and
and
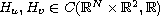 .
Under conditions that
.
Under conditions that
 or
or
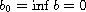 and
and
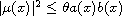 with
with
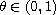 and some mild assumptions on
and some mild assumptions on
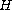 ,
we show that the system has at least one
nontrivial solution provided that
,
we show that the system has at least one
nontrivial solution provided that
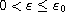 , where the bound
, where the bound
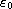 is
formulated in terms of N, a, b and H.
is
formulated in terms of N, a, b and H.

