Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 241, pp. 1-16.
Spectrum for anisotropic equations involving weights and variable exponents
Ionela-Loredana Stancut
Abstract:
We study the problem
![$$
-\sum_{i=1}^{N}\Big[\partial_{x_{i}}\Big(|\partial_{x_{i}}u|^{p_{i}(x)-2}
\partial_{x_{i}}u\Big)
+|u|^{p_{i}(x)-2}u\Big]+|u|^{q(x)-2}u
=\lambda g(x)|u|^{r(x)-2}u
$$](gifs/aa.gif)
in
 ,
,
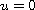 on
on
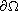 ,
where
,
where
 is a bounded domain in
is a bounded domain in
 (
(
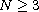 ),
with smooth boundary,
),
with smooth boundary,
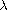 is a
positive real number, the functions
is a
positive real number, the functions
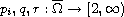 are Lipschitz continuous,
are Lipschitz continuous,
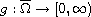 is measurable and
these fulfill certain conditions. The main result of this paper establish
the existence of two positive constants
is measurable and
these fulfill certain conditions. The main result of this paper establish
the existence of two positive constants
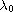 and
and
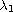 with
with
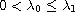 such that any
such that any
 is an eigenvalue, while any
is an eigenvalue, while any
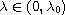 is not an eigenvalue of
our problem.
is not an eigenvalue of
our problem.
Submitted June 26, 2014. Published November 18, 2014.
Math Subject Classifications: 35D30, 35J60, 58E05.
Key Words: p(.)-Laplace operator; anisotropic variable exponent Sobolev space;
critical point; weak solution; eigenvalue.
Show me the PDF file (274 KB),
TEX file, and other files for this article.
 |
Ionela-Loredana Stancut
Department of Mathematics
University of Craiova
200585, Romania
email: stancutloredana@yahoo.com
|
|---|
Return to the EJDE web page
![$$
-\sum_{i=1}^{N}\Big[\partial_{x_{i}}\Big(|\partial_{x_{i}}u|^{p_{i}(x)-2}
\partial_{x_{i}}u\Big)
+|u|^{p_{i}(x)-2}u\Big]+|u|^{q(x)-2}u
=\lambda g(x)|u|^{r(x)-2}u
$$](gifs/aa.gif)
 ,
,
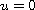 on
on
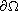 ,
where
,
where
 is a bounded domain in
is a bounded domain in
 (
(
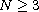 ),
with smooth boundary,
),
with smooth boundary,
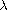 is a
positive real number, the functions
is a
positive real number, the functions
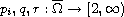 are Lipschitz continuous,
are Lipschitz continuous,
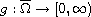 is measurable and
these fulfill certain conditions. The main result of this paper establish
the existence of two positive constants
is measurable and
these fulfill certain conditions. The main result of this paper establish
the existence of two positive constants
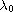 and
and
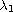 with
with
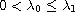 such that any
such that any
 is an eigenvalue, while any
is an eigenvalue, while any
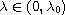 is not an eigenvalue of
our problem.
is not an eigenvalue of
our problem.
