Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 239, pp. 1-17.
Pohozaev-type inequalities and nonexistence results for non C^2
solutions of p(x)-Laplacian equations
Gabriel Lopez
Abstract:
In this article we obtain a Pohozaev-type inequality for Sobolev spaces
with variable exponents. This inequality is used for proving the nonexistence
of nontrivial weak solutions for the Dirichlet problem
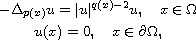
with non-standard growth. Our results extend those obtained by Otani [16].
Submitted September 6, 2014. Published November 14, 2014.
Math Subject Classifications: 35D05, 35J60, 58E05.
Key Words: Pohozaev-type inequality; p(x)-Laplace operator;
Sobolev spaces with variable exponents.
Show me the PDF file (290 KB),
TEX file, and other files for this article.
 |
Gabriel López G.
Universidad Autónoma Metropolitana
México D.F., México
email: gabl@xanum.uam.mx
|
|---|
Return to the EJDE web page