Let
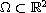 be a bounded domain with the same area as the
unit disk
be a bounded domain with the same area as the
unit disk
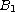 and let
and let
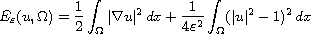
be the Ginzburg-Landau functional. Denote by
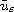 the radial solution to the Euler equation associated to the problem
the radial solution to the Euler equation associated to the problem
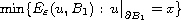 and by
and by
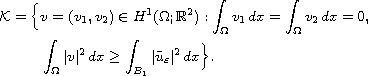
In this note we prove that
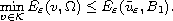
Barbara Brandolini, Francesco Chiacchio
Abstract:
Let
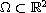 be a bounded domain with the same area as the
unit disk
be a bounded domain with the same area as the
unit disk
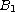 and let
and let
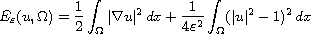
be the Ginzburg-Landau functional. Denote by
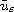 the radial solution to the Euler equation associated to the problem
the radial solution to the Euler equation associated to the problem
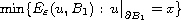 and by
and by
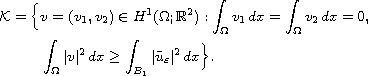
In this note we prove that
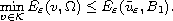
Submitted September 15, 2014. Published October 21, 2014.
Math Subject Classifications: 35Q56, 35J15.
Key Words: Ginzburg-Landau functional, Szego-Weinberger inequality.
Show me the PDF file (171 KB), TEX file, and other files for this article.
 |
Barbara Brandolini Dipartimento di Matematica e Applicazioni "R. Caccioppoli" Universitá degli Studi di Napoli "Federico II" Complesso Monte S. Angelo, via Cintia - 80126 Napoli, Italy email: brandolini@unina.it |
|---|---|
 |
Francesco Chiacchio Dipartimento di Matematica e Applicazioni "R. Caccioppoli" Universitá degli Studi di Napoli "Federico II" Complesso Monte S. Angelo, via Cintia - 80126 Napoli, Italy email: francesco.chiacchio@unina.it |
Return to the EJDE web page