Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 219, pp. 1-13.
Semilinear elliptic equations involving a gradient term in unbounded domains
V. Raghavendra, Rasmita Kar
Abstract:
In this article, we study the existence of a classical solution of
semilinear elliptic BVP involving gradient term of the type
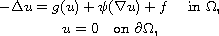
where
 is a (not necessarily bounded) domain in
is a (not necessarily bounded) domain in
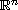 ,
,
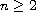 with smooth boundary
with smooth boundary
 .
.
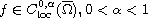 ,
,
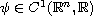 and
and
 satisfies certain conditions
(well known in the literature as "jumping nonlinearity").
satisfies certain conditions
(well known in the literature as "jumping nonlinearity").
Submitted October 10, 2011. Published October 16, 2014.
Math Subject Classifications: 35J65, 35J25.
Key Words: Monotone method; Ambrosetti-prodi type problem; unbounded domain.
Show me the PDF file (273 KB),
TEX file, and other files for this article.
 |
Venkataramanarao Raghavendra
Department of Mathematics and Statistics
Indian Institute of Technology
Kanpur 208016, India
email: vrag@iitk.ac.in
|
|---|
 |
Rasmita Kar
Department of Mathematics and Statistics
Indian Institute of Technology
Kanpur 208016, India
email: rasmitak6@gmail.com
|
|---|
Return to the EJDE web page
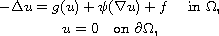
 is a (not necessarily bounded) domain in
is a (not necessarily bounded) domain in
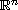 ,
,
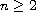 with smooth boundary
with smooth boundary
 .
.
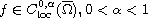 ,
,
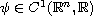 and
and
 satisfies certain conditions
(well known in the literature as "jumping nonlinearity").
satisfies certain conditions
(well known in the literature as "jumping nonlinearity").

