Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 214, pp. 1-10.
Sturm-Picone type theorems for second-order nonlinear elliptic
differential equations
Aydin Tiryaki
Abstract:
The aim of this article is to give Sturm-Picone type theorems for
the pair of second order nonlinear elliptic differential equations
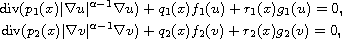
where
 denotes the Euclidean length and
denotes the Euclidean length and
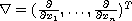 (the superscript T
denotes the transpose). Our results include some earlier results
and generalize to n-dimensions well-known comparison theorems
given by Sturm, Picone and Leighton ]26.37]
which play a key role in the qualitative behavior of solutions.
By using generalization of n dimensional Leigton's comparison theorem,
an oscillation result is given as an application.
(the superscript T
denotes the transpose). Our results include some earlier results
and generalize to n-dimensions well-known comparison theorems
given by Sturm, Picone and Leighton ]26.37]
which play a key role in the qualitative behavior of solutions.
By using generalization of n dimensional Leigton's comparison theorem,
an oscillation result is given as an application.
Submitted July 16, 2014. Published October 14, 2014.
Math Subject Classifications: 35B05.
Key Words: Comparison theorem; Sturm-Picone theorem; half-linear equations,
variational lemma; elliptic equations; oscillation.
Show me the PDF file (244 KB),
TEX file, and other files for this article.
 |
Aydin Tiryaki
Department of Mathematics and Computer Sciences
Faculty of Arts and Sciences, Izmir University
35350 Uckuyular, Izmir, Turkey
email: aydin.tiryaki@izmir.edu.tr
|
|---|
Return to the EJDE web page
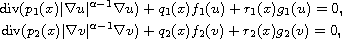
 denotes the Euclidean length and
denotes the Euclidean length and
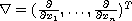 (the superscript T
denotes the transpose). Our results include some earlier results
and generalize to n-dimensions well-known comparison theorems
given by Sturm, Picone and Leighton ]26.37]
which play a key role in the qualitative behavior of solutions.
By using generalization of n dimensional Leigton's comparison theorem,
an oscillation result is given as an application.
(the superscript T
denotes the transpose). Our results include some earlier results
and generalize to n-dimensions well-known comparison theorems
given by Sturm, Picone and Leighton ]26.37]
which play a key role in the qualitative behavior of solutions.
By using generalization of n dimensional Leigton's comparison theorem,
an oscillation result is given as an application.
