This work concerns the asymptotic behavior of solutions to the differential equation
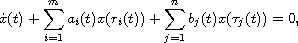
where
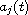 and
and
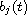 are real-valued
continuous functions and
are real-valued
continuous functions and
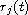 and
and
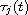 are non-negative functions such that
are non-negative functions such that
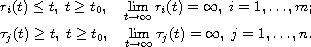
Sandra Pinelas
Abstract:
This work concerns the asymptotic behavior of solutions to the
differential equation
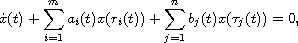
where
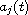 and
and
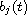 are real-valued
continuous functions and
are real-valued
continuous functions and
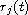 and
and
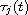 are non-negative functions such that
are non-negative functions such that
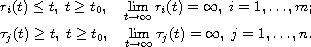
Submitted May 5, 2014. Published October 10, 2014.
Math Subject Classifications: 34K06, 34D04, 47H10.
Key Words: Differential equations; fixed point; asymptotic behavior.
Show me the PDF file (212 KB), TEX file, and other files for this article.
 |
Sandra Pinelas Academia Militar Departamento de Ciências Exatas e Naturais Conde Castro Guimarães, Amadora, Portugal email: sandra.pinelas@gmail.com |
|---|
Return to the EJDE web page