Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 208, pp. 1-10.
Feynman-Kac theorem in Hilbert spaces
Irina V. Melnikova, Valentina S. Parfenenkova
Abstract:
In this article we study the relationship between solutions to Cauchy problems
for the abstract stochastic differential equation
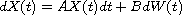 and solutions to Cauchy problems (backward and forward)
for the infinite dimensional deterministic partial differential equation
and solutions to Cauchy problems (backward and forward)
for the infinite dimensional deterministic partial differential equation
![$$
\pm\frac{\partial g}{\partial t}(t,x) + \frac{\partial g}{\partial x}(t,x)Ax
+ \frac{1}{2}\hbox{Tr}[(BQ^{1/2})^*
\frac{\partial^2 g}{\partial x^2}(t,x) (BQ^{1/2})] = 0,
$$](gifs/ab.gif)
where g is the probability characteristic
![$g=\mathbb{E}^{t,x}[h(X(T))]$](gifs/ac.gif) in the backward case and
in the backward case and
![$g=\mathbb{E}^{0,x}[h(X(t))]$](gifs/ad.gif) in the forward case.
This relationship, that is the inifinite dimensional Feynman-Kac theorem,
is proved in both directions: from stochastic to deterministic and from
deterministic to stochastic. Special attention is given to the definition and
interpretation of objects in the equations.
in the forward case.
This relationship, that is the inifinite dimensional Feynman-Kac theorem,
is proved in both directions: from stochastic to deterministic and from
deterministic to stochastic. Special attention is given to the definition and
interpretation of objects in the equations.
Submitted February 20, 2014. Published October 7, 2014.
Math Subject Classifications: 47D06, 60G15, 60H30.
Key Words: Semigroups of operators; infinite dimensional stochastic equations;
diffusion processes; Kolmogorov equations.
Show me the PDF file (229 KB),
TEX file, and other files for this article.
 |
Irina V. Melnikova
Ural Federal University
Lenin av. 51, 620083 Ekaterinburg, Russia
email: Irina.Melnikova@usu.ru
|
|---|
 |
Valentina S. Parfenenkova
Ural Federal University
Lenin av. 51, 620083 Ekaterinburg, Russia
email: vika8887@e1.ru
|
|---|
Return to the EJDE web page
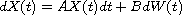 and solutions to Cauchy problems (backward and forward)
for the infinite dimensional deterministic partial differential equation
and solutions to Cauchy problems (backward and forward)
for the infinite dimensional deterministic partial differential equation
![$$
\pm\frac{\partial g}{\partial t}(t,x) + \frac{\partial g}{\partial x}(t,x)Ax
+ \frac{1}{2}\hbox{Tr}[(BQ^{1/2})^*
\frac{\partial^2 g}{\partial x^2}(t,x) (BQ^{1/2})] = 0,
$$](gifs/ab.gif)
![$g=\mathbb{E}^{t,x}[h(X(T))]$](gifs/ac.gif) in the backward case and
in the backward case and
![$g=\mathbb{E}^{0,x}[h(X(t))]$](gifs/ad.gif) in the forward case.
This relationship, that is the inifinite dimensional Feynman-Kac theorem,
is proved in both directions: from stochastic to deterministic and from
deterministic to stochastic. Special attention is given to the definition and
interpretation of objects in the equations.
in the forward case.
This relationship, that is the inifinite dimensional Feynman-Kac theorem,
is proved in both directions: from stochastic to deterministic and from
deterministic to stochastic. Special attention is given to the definition and
interpretation of objects in the equations.

