Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 206, pp. 1-14.
Precise asymptotic behavior of strongly decreasing solutions
of first-order nonlinear functional differential equations
George E. Chatzarakis, Kusano Takasi, Ioannis P. Stavroulakis
Abstract:
In this article, we study the asymptotic behavior of strongly decreasing
solutions of the first-order nonlinear functional differential equation
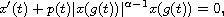
where
 is a positive constant such that
is a positive constant such that
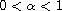 ,
p(t) is a
positive continuous function on
,
p(t) is a
positive continuous function on
 ,
a>0 and g(t) is a
positive continuous function on
,
a>0 and g(t) is a
positive continuous function on
 such that
such that
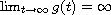 . Conditions which guarantee the existence
of strongly decreasing solutions are established, and theorems are stated on the
asymptotic behavior of such solutions, at infinity. The problem it is
studied in the framework of regular variation, assuming that the coefficient
p(t) is a regularly varying function, and focusing on strongly decreasing
solutions that are regularly varying. In addition, g(t) is required to
satisfy the condition
. Conditions which guarantee the existence
of strongly decreasing solutions are established, and theorems are stated on the
asymptotic behavior of such solutions, at infinity. The problem it is
studied in the framework of regular variation, assuming that the coefficient
p(t) is a regularly varying function, and focusing on strongly decreasing
solutions that are regularly varying. In addition, g(t) is required to
satisfy the condition

Examples illustrating the results are also given.
Submitted June 26, 2014. Published October 2, 2014.
Math Subject Classifications: 34C11, 26A12
Key Words: Functional differential equation; strongly decreasing solution;
regularly varying function; slowly varying solution.
Show me the PDF file (272 KB),
TEX file, and other files for this article.
 |
George E. Chatzarakis
Department of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education (ASPETE)
14121, N. Heraklio, Athens, Greece
email: geaxatz@otenet.gr, gea.xatz@aspete.gr
|
|---|
| |
Kusano Takasi
Professor Emeritus at: Department of Mathematics
Faculty of Science, Hiroshima University
Higashi-Hiroshima 739-8526, Japan
email: kusanot@zj8.so-net.ne.jp
|
|---|
 |
Ioannis P. Stavroulakis
Department of Mathematics, University of Ioannina
451 10 Ioannina, Greece
email: ipstav@cc.uoi.gr
|
|---|
Return to the EJDE web page
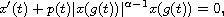
 is a positive constant such that
is a positive constant such that
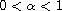 ,
p(t) is a
positive continuous function on
,
p(t) is a
positive continuous function on
 ,
a>0 and g(t) is a
positive continuous function on
,
a>0 and g(t) is a
positive continuous function on
 such that
such that
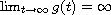 . Conditions which guarantee the existence
of strongly decreasing solutions are established, and theorems are stated on the
asymptotic behavior of such solutions, at infinity. The problem it is
studied in the framework of regular variation, assuming that the coefficient
p(t) is a regularly varying function, and focusing on strongly decreasing
solutions that are regularly varying. In addition, g(t) is required to
satisfy the condition
. Conditions which guarantee the existence
of strongly decreasing solutions are established, and theorems are stated on the
asymptotic behavior of such solutions, at infinity. The problem it is
studied in the framework of regular variation, assuming that the coefficient
p(t) is a regularly varying function, and focusing on strongly decreasing
solutions that are regularly varying. In addition, g(t) is required to
satisfy the condition


